题目内容
某研究性学习小组探究用单摆测定当地的重力加速度,进行了如下实验:
(1)用单摆测重力加速度的实验中,为使周期的测量尽可能准确,则计时位置应在单摆摆动到
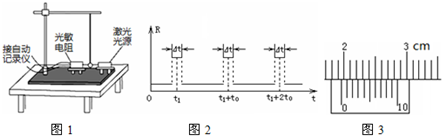
(2)为了将人工记录振动次数改为自动记录振动次数,在摆球运动最低点的左、右两侧分别放置一激光光源与光敏电阻,细激光束与球心等高,如图1所示,光敏电阻与某一自动记录仪相连,该仪器显示的光敏电阻阻值R随时间t变化图线如2所示,则该单摆的振动周期为
(3)用主尺最小分度为1mm,游标上有20个分度的卡尺测量金属球的直径,结果如图3所示,可以读出此金属球的直径为
(4)研究性学习小组测得悬线长度L、摆球直径d、全振动次数n、完成n次全振动的时间t,则当地的重力加速度g=
;(用字母表示)
(1)用单摆测重力加速度的实验中,为使周期的测量尽可能准确,则计时位置应在单摆摆动到
最低点
最低点
(选填“最高点”、“最低点”),同时测量摆球摆动30~50次的时间,算出单摆的周期.(2)为了将人工记录振动次数改为自动记录振动次数,在摆球运动最低点的左、右两侧分别放置一激光光源与光敏电阻,细激光束与球心等高,如图1所示,光敏电阻与某一自动记录仪相连,该仪器显示的光敏电阻阻值R随时间t变化图线如2所示,则该单摆的振动周期为
2t0
2t0
.若保持悬点到小球顶点的绳长不变,改用密度不变,直径是原小球直径2倍的另一小球进行实验,单摆的摆角不变,则该单摆的周期将变大
变大
,(填“变大”、“不变”或“变小”).(3)用主尺最小分度为1mm,游标上有20个分度的卡尺测量金属球的直径,结果如图3所示,可以读出此金属球的直径为
19.6
19.6
mm.(4)研究性学习小组测得悬线长度L、摆球直径d、全振动次数n、完成n次全振动的时间t,则当地的重力加速度g=
4π2n2(L+
| ||
| t2 |
4π2n2(L+
| ||
| t2 |

分析:(1)单摆最低点速度最大,在此时计时误差最小.
(2)在一个周期内两次经过平衡位置,根据该特点结合图象得出单摆的周期.根据单摆的周期公式T=2π
判断周期的变化.
(3)游标卡尺的读数等于主尺读数加上游标读数,不需估读.
(4)根据单摆的周期公式T=2π
推导重力加速度的表达式.
(2)在一个周期内两次经过平衡位置,根据该特点结合图象得出单摆的周期.根据单摆的周期公式T=2π
|
(3)游标卡尺的读数等于主尺读数加上游标读数,不需估读.
(4)根据单摆的周期公式T=2π
|
解答:解:(1)单摆在最低点速度最大,最高点速度为0,在最低点计时误差最小.
(2)单摆在一个周期内两次经过平衡位置,每次经过平衡位置,单摆会挡住细激光束,从R-t图线可知周期为2t0.摆长等于摆线的长度加上小球的半径,根据单摆的周期公式T=2π
,摆长变大,所以周期变大.
(3)游标卡尺主尺读数为19mm,游标读数为0.1×6=0.6mm,所以最终读数为19.6mm.
(4)摆长l=L+
,周期T=
,根据单摆的周期公式T=2π
,g=
=
.
(1)最低点 (2)2t0,变大 (3)19.6 (4)
(2)单摆在一个周期内两次经过平衡位置,每次经过平衡位置,单摆会挡住细激光束,从R-t图线可知周期为2t0.摆长等于摆线的长度加上小球的半径,根据单摆的周期公式T=2π
|
(3)游标卡尺主尺读数为19mm,游标读数为0.1×6=0.6mm,所以最终读数为19.6mm.
(4)摆长l=L+
| d |
| 2 |
| t |
| n |
|
| 4π2l |
| T2 |
4π2n2(L+
| ||
| t2 |
(1)最低点 (2)2t0,变大 (3)19.6 (4)
4π2n2(L+
| ||
| t2 |
点评:解决本题的关键掌握单摆的周期公式T=2π
.知道单摆的摆长等于摆线的长度加上摆球的半径.
|

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目