题目内容
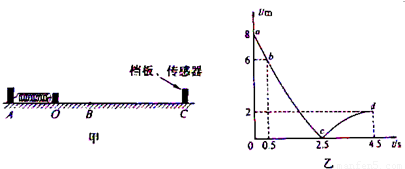
图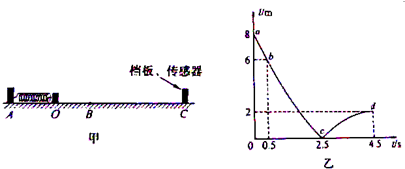 甲为一水平面,其AB段光滑,BC段粗糙,一刚性挡板固定在C处.一轻弹簧左端固定,自然伸长时右端处于O点.一个质量为m=0.5kg的小滑块(可视为质点)从O点左侧x=0.1m处由静止开始释放,再压缩的弹簧作用下开始运动,当小物块运动到O点时小物块与轻弹簧分离,当小物块运动到小物块与C处与固定挡板碰撞(碰撞过程无能量损失,碰撞时间可忽略).在C处有一位移传感器,可测量与C点的距离.若小物块通过O点时开始计时,传感器显示的距离随时间t变化的情况如图乙所示(图中ab为直线,bc、cd为曲线).已知弹簧被压缩后获得的弹性势能可用公式EP=
甲为一水平面,其AB段光滑,BC段粗糙,一刚性挡板固定在C处.一轻弹簧左端固定,自然伸长时右端处于O点.一个质量为m=0.5kg的小滑块(可视为质点)从O点左侧x=0.1m处由静止开始释放,再压缩的弹簧作用下开始运动,当小物块运动到O点时小物块与轻弹簧分离,当小物块运动到小物块与C处与固定挡板碰撞(碰撞过程无能量损失,碰撞时间可忽略).在C处有一位移传感器,可测量与C点的距离.若小物块通过O点时开始计时,传感器显示的距离随时间t变化的情况如图乙所示(图中ab为直线,bc、cd为曲线).已知弹簧被压缩后获得的弹性势能可用公式EP=
kx2计算,k为弹簧的劲度系数,x为弹簧的形变量.求:
(1)小物块到达B点时的速度;
(2)弹簧的劲度系数;
(3)小物块与水平面BC段间的动摩擦因数.
 甲为一水平面,其AB段光滑,BC段粗糙,一刚性挡板固定在C处.一轻弹簧左端固定,自然伸长时右端处于O点.一个质量为m=0.5kg的小滑块(可视为质点)从O点左侧x=0.1m处由静止开始释放,再压缩的弹簧作用下开始运动,当小物块运动到O点时小物块与轻弹簧分离,当小物块运动到小物块与C处与固定挡板碰撞(碰撞过程无能量损失,碰撞时间可忽略).在C处有一位移传感器,可测量与C点的距离.若小物块通过O点时开始计时,传感器显示的距离随时间t变化的情况如图乙所示(图中ab为直线,bc、cd为曲线).已知弹簧被压缩后获得的弹性势能可用公式EP=
甲为一水平面,其AB段光滑,BC段粗糙,一刚性挡板固定在C处.一轻弹簧左端固定,自然伸长时右端处于O点.一个质量为m=0.5kg的小滑块(可视为质点)从O点左侧x=0.1m处由静止开始释放,再压缩的弹簧作用下开始运动,当小物块运动到O点时小物块与轻弹簧分离,当小物块运动到小物块与C处与固定挡板碰撞(碰撞过程无能量损失,碰撞时间可忽略).在C处有一位移传感器,可测量与C点的距离.若小物块通过O点时开始计时,传感器显示的距离随时间t变化的情况如图乙所示(图中ab为直线,bc、cd为曲线).已知弹簧被压缩后获得的弹性势能可用公式EP=| 1 | 2 |
(1)小物块到达B点时的速度;
(2)弹簧的劲度系数;
(3)小物块与水平面BC段间的动摩擦因数.
分析:(1)由题意及图象可知:小物块在OB段做运动直线运动,根据v=
即可求解;
(2)取弹簧和小物块为系统,在小物块由静止释放到小物块到达O点的过程中,机械能守恒,根据机械能守恒定律即可求解;
(3)由题意及图象可知,小物块通过B点后做匀减速直线运动,根据动能定理列式即可求解.
| x |
| t |
(2)取弹簧和小物块为系统,在小物块由静止释放到小物块到达O点的过程中,机械能守恒,根据机械能守恒定律即可求解;
(3)由题意及图象可知,小物块通过B点后做匀减速直线运动,根据动能定理列式即可求解.
解答:解:(1)由题意及图象可知:小物块在OB段做运动直线运动,x1=2m,t1=0.5s,则小物块的速度:
v=
=4m/s
(2)取弹簧和小物块为系统,在小物块由静止释放到小物块到达O点的过程中,机械能守恒,则:
kx2=
mv2
解得:k=800N/m
(3)由题意及图象可知,小物块通过B点后做匀减速直线运动,且x2=6m,与挡板碰撞后反向运动一段距离后停止,且x3=2m,根据动能定理得:
-μmg(x2-x3)=0-
mv2
解得:μ=0.2
答:(1)小物块到达B点时的速度为4m/s;
(2)弹簧的劲度系数为800N/m;
(3)小物块与水平面BC段间的动摩擦因数为0.2.
v=
| x1 |
| t1 |
(2)取弹簧和小物块为系统,在小物块由静止释放到小物块到达O点的过程中,机械能守恒,则:
| 1 |
| 2 |
| 1 |
| 2 |
解得:k=800N/m
(3)由题意及图象可知,小物块通过B点后做匀减速直线运动,且x2=6m,与挡板碰撞后反向运动一段距离后停止,且x3=2m,根据动能定理得:
-μmg(x2-x3)=0-
| 1 |
| 2 |
解得:μ=0.2
答:(1)小物块到达B点时的速度为4m/s;
(2)弹簧的劲度系数为800N/m;
(3)小物块与水平面BC段间的动摩擦因数为0.2.
点评:本题主要考查了动能定理及机械能守恒定律的直接应用,要求同学们能根据图象得出有效信息,难度适中.

练习册系列答案
相关题目
 计算,k为弹簧的劲度系数,x为弹簧的形变量.求:
计算,k为弹簧的劲度系数,x为弹簧的形变量.求: