题目内容
 如图所示,空气中一块圆截异型玻璃砖,折射率为
如图所示,空气中一块圆截异型玻璃砖,折射率为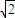 ,现有一束细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行返回,角AOB为135°,圆半径为r.则入射点P距圆心O的距离为( )
,现有一束细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行返回,角AOB为135°,圆半径为r.则入射点P距圆心O的距离为( )A.rsin15°
B.rsin7.5°
C.

D.
 r
r
【答案】分析:作出光路图,由几何知识得到光线从OB射出时的折射角,由折射定律求出光线在OB面的入射角,根据几何知识求出∠PCD,由反射光路的对称性,得到∠PCO,再求解入射点P距圆心O的距离OP.
解答:解:由图可知,光线从OB射出时的折射角为45°,设光线在OB面的入射角为α.
由折射定律得 ,则α=30°,即光在OB面的入射角为30°,所以∠PCD=360°-90°-(90°+30°)-135°=15°,故根据对称性得知
,则α=30°,即光在OB面的入射角为30°,所以∠PCD=360°-90°-(90°+30°)-135°=15°,故根据对称性得知
∠PCO=7.5°,所以OP=rsin7.5°,故B正确.
故选B.
点评:考查光的反射和折射,主要问题是运用几何知识分析角度关系,求出折射角和入射角.
解答:解:由图可知,光线从OB射出时的折射角为45°,设光线在OB面的入射角为α.
由折射定律得
 ,则α=30°,即光在OB面的入射角为30°,所以∠PCD=360°-90°-(90°+30°)-135°=15°,故根据对称性得知
,则α=30°,即光在OB面的入射角为30°,所以∠PCD=360°-90°-(90°+30°)-135°=15°,故根据对称性得知
∠PCO=7.5°,所以OP=rsin7.5°,故B正确.
故选B.
点评:考查光的反射和折射,主要问题是运用几何知识分析角度关系,求出折射角和入射角.

练习册系列答案
相关题目
 (2013?开封一模) 如图所示,空气中一块圆截异型玻璃砖,折射率为
(2013?开封一模) 如图所示,空气中一块圆截异型玻璃砖,折射率为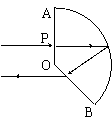
 如图所示,空气中一块圆截异型玻璃砖,折射率为
如图所示,空气中一块圆截异型玻璃砖,折射率为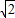 ,现有一束细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行返回,角AOB为135°,圆半径为r.则入射点P距圆心O的距离为( )
,现有一束细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行返回,角AOB为135°,圆半径为r.则入射点P距圆心O的距离为( )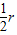
 r
r 如图所示,空气中一块圆截异型玻璃砖,折射率为
如图所示,空气中一块圆截异型玻璃砖,折射率为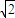 ,现有一束细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行返回,角AOB为135°,圆半径为r.则入射点P距圆心O的距离为( )
,现有一束细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行返回,角AOB为135°,圆半径为r.则入射点P距圆心O的距离为( )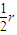
 r
r