题目内容
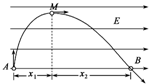 在电场方向水平向右的匀强电场中,一带电小球从A点竖直向上抛出,其运动的轨迹如图所示.小球运动的轨迹上A、B两点在同一水平线上,M为轨迹的最高点.小球抛出时的动能为8.0J,在M点的动能为6.0J,不计空气的阻力.求:
在电场方向水平向右的匀强电场中,一带电小球从A点竖直向上抛出,其运动的轨迹如图所示.小球运动的轨迹上A、B两点在同一水平线上,M为轨迹的最高点.小球抛出时的动能为8.0J,在M点的动能为6.0J,不计空气的阻力.求:(1)小球水平位移x1与x2的比值;
(2)小球落到B点时的动能EkB.
(3)小球从A点运动到B点的过程中最小动能Ekmin?
分析:(1)小球在竖直方向上做竖直上抛运动,根据对称性可知从A点至M点和从M点至B点的时间t相等.小球在水平方向上做初速为零的匀加速运动,由运动学公式位移公式,运用比例法求出x1与x2之比;
(2)分别研究A到M和A到B水平方向的分运动,由运动学公式速度位移关系式求出小球到达B点的速度,即可得到动能EKB;
(3)根据速度的合成得到动能与时间的关系式,运用数学知识求极值,得到小球动能的最小值.
(2)分别研究A到M和A到B水平方向的分运动,由运动学公式速度位移关系式求出小球到达B点的速度,即可得到动能EKB;
(3)根据速度的合成得到动能与时间的关系式,运用数学知识求极值,得到小球动能的最小值.
解答:解:(1)小球在竖直方向上做竖直上抛运动,根据对称性得知,从A点至M点和从M点至B点的时间t相等.
小球在水平方向上做初速为零的匀加速直线运动,设加速度为a,则
x1=
at2
x2=
a(2t)2-
at2=
at2
所以
=
(2)小球从A到M,水平方向上电场力做功W电=Eqx1=6J,
则从A到B水平方向上电场力做功W电′=Eq(x1+x2)=4W电=24J
则由能量守恒可知,小球运动到B点时的动能为EkB=Ek0+4W电=8+24J=32J
(3)由题,
mvA2=8J,
得vA=
又竖直方向上,有vA=gt=
t,
所以
=
t,①
mvM2=6J,
得vM=
在水平方向上,有 vM=at=
t,
则得
=
t,②
所以②:①得
=
设小球运动时间为t时动能为Ek,则
Ek=
m(v0-gt)2+
m(at)2
化简为 (g2+a2)t2-2v0gt+v02-
=0
当△=0时有极值,
则4v02g2-4(g2+a2)(v02-
)=0
得Ek=
Ek0
由
=
得a=
g
即Ekmin=
Ek0=
×8J=
J.
答:(1)小球水平位移x1与x2的比值为1:3.
(2)小球落到B点时的动能EkB=32J.
(3)小球从A点运动到B点的过程中最小动能Ekmin为
J.
小球在水平方向上做初速为零的匀加速直线运动,设加速度为a,则
x1=
| 1 |
| 2 |
x2=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以
| x1 |
| x2 |
| 1 |
| 3 |
(2)小球从A到M,水平方向上电场力做功W电=Eqx1=6J,
则从A到B水平方向上电场力做功W电′=Eq(x1+x2)=4W电=24J
则由能量守恒可知,小球运动到B点时的动能为EkB=Ek0+4W电=8+24J=32J
(3)由题,
| 1 |
| 2 |
得vA=
| 4 | ||
|
又竖直方向上,有vA=gt=
| G |
| m |
所以
| 4 | ||
|
| G |
| m |
| 1 |
| 2 |
得vM=
| ||
|
在水平方向上,有 vM=at=
| F |
| m |
则得
| ||
|
| F |
| m |
所以②:①得
| F |
| G |
| ||
| 2 |
设小球运动时间为t时动能为Ek,则
Ek=
| 1 |
| 2 |
| 1 |
| 2 |
化简为 (g2+a2)t2-2v0gt+v02-
| 2Ek |
| m |
当△=0时有极值,
则4v02g2-4(g2+a2)(v02-
| 2Ek |
| m |
得Ek=
| a2 |
| g2+a2 |
由
| F |
| G |
| ||
| 2 |
得a=
| ||
| 2 |
即Ekmin=
| 3 |
| 7 |
| 3 |
| 7 |
| 24 |
| 7 |
答:(1)小球水平位移x1与x2的比值为1:3.
(2)小球落到B点时的动能EkB=32J.
(3)小球从A点运动到B点的过程中最小动能Ekmin为
| 24 |
| 7 |
点评:本题运用运动的合成和分解法处理,抓住竖直方向上运动的对称性得到时间关系是关键.对于第3题,也可以求出重力加速度与电场力加速度形成合加速度,当速度方向与合加速度方向垂直时速度最小,动能最小,再由运动学公式和牛顿第二定律结合求解.

练习册系列答案
相关题目
 在电场方向水平向右的匀强电场中,一带电小球从A点竖直向上抛出,其运动的轨迹如图所示.小球运动的轨迹上A、B两点在同一水平线上,M为轨迹的最高点.小球抛出时的动能为8.0J,在M点的动能为6.0J,不计空气的阻力.则( )
在电场方向水平向右的匀强电场中,一带电小球从A点竖直向上抛出,其运动的轨迹如图所示.小球运动的轨迹上A、B两点在同一水平线上,M为轨迹的最高点.小球抛出时的动能为8.0J,在M点的动能为6.0J,不计空气的阻力.则( )

