题目内容
如图7所示,质量为m的物体,在倾角为θ的斜面上向上以加速度a做匀加速直线运动,物体与斜面间的动摩擦因数为μ,求作用在物体上的水平向右的力F的大小.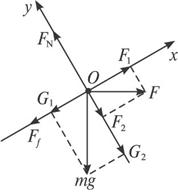
图7
F=(mgsinθ+μmgcosθ+ma)/(cosθ-μsinθ)
解析:物体受重力mg、支持力FN、滑动摩擦力Ff和推力F沿斜面向上做匀加速运动,可将力F分解为垂直于斜面方向和沿斜面方向的力,则垂直于斜面方向的合外力为零,沿斜面方向的合外力为ma.
建立如下图所示直角坐标系xOy,将重力及推力沿x轴和y轴分解,则:

G1=mgsinθ G2=mgcosθ
F1=Fcosθ F2=Fsinθ
由牛顿第二定律
在x轴上
∑Fx=F1-G1-Ff=ma
即Fcosθ-mgsinθ-Ff=ma ①
在y轴上∑Fy=FN-F2-G2=0
即FN-Fsinθ-mgcosθ =0 ②
由摩擦力公式得Ff=μFN ③
联立①②③解得
F=![]() .
.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目