题目内容
如图所示，
是位于足够大的绝缘光滑水平桌面内的平面直角坐标系，虚线MN是∠
的角平分线．在MN的左侧区域，存在着沿
轴负方向、场强为E的匀强电场；在MN的右侧区域，存在着方向竖直向下、磁感应强度为B的匀强磁场，现有一带负电的小球
从y轴上的P(0，L)点，在电场力作用下由静止开始运动，小球到达虚线MN上的Q点时与另一个不带电的静止小球
发生碰撞，碰后两小球粘合在一起进入磁场，它们穿出磁场的位置恰好在O点．若、两小球的质量相等且均可视为质点，、碰撞过程中无电荷量损失，不计重力作用．求：
（1）小球的比荷
（即电荷量与质量之比）；
（2）过O点后，粘在一起的两个小球再次到达虚线MN上的位置坐标（结果用E、B、L表示）．
（1）设的质量为
、电荷量为
，与碰撞前后的速度大小分别为
、
，碰后两球在磁场中运动的轨道半径为R．在电场中做匀加速直线运动，由动能定理得：
（2分）
与碰撞中动量守恒，有：
（2分）解得
（2分）
由题意知，Q点的位置坐标一定是（L，L），且碰后两球在磁场中做匀速圆周运动的圆心O1一定在轴上，如图，所以R=L（2分）由洛伦兹力提供向心力有：
（2分）故有
（2分）
（2）过O点后，两球以沿
轴正方向的初速度在电场中做类平抛运动，设它们再次到达虚线MN上的位置坐标为
，在电场中运动的时间为
由运动学公式的：
（2分）
（2分）且
（2分）解得：
，所以两球再次到达虚线MN上的位置坐标是
（2分）
练习册系列答案
相关题目
如图所示，两条足够长的互相平行的光滑金属导轨位于水平面内，距离为L=0.5m．在导轨的一端分别接有阻值均为0.6Ω的电阻R1、R2，在x≥0处有一与水平面垂直的匀强磁场，磁感应强度B=1T．一质量m=0.2kg的金属杆垂直放置在导轨上，金属直杆的电阻是r=0.2Ω，其他电阻忽略不计，金属直杆以一定的初速度v0=4m/s进入磁场，同时受到沿x轴正方向的恒力F=3.5N的作用，在x=2m处速度达到稳定．求：
如图所示，两条足够长的互相平行的光滑金属导轨位于水平面内，距离为L=0.5m．在导轨的一端接有阻值为0.8Ω的电阻R，在x≥0处有一与水平面垂直的匀强磁场，磁感应强度B=1T．一质量m=0.2kg的金属杆垂直放置在导轨上，金属直杆的电阻是r=0.2Ω，其他电阻忽略不计，金属直杆以一定的初速度v0=4m/s进入磁场，同时受到沿x轴正方向的恒力F=3.5N的作用，在x=6m处速度达到稳定．求：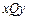
是位于足够大的绝缘光滑水平桌面内的平面直角坐标系，虚线MN是∠
的角平分线．在MN的左侧区域，存在着沿
轴负方向、场强为E的匀强电场；在MN的右侧区域，存在着方向竖直向下、磁感应强度为B的匀强磁场，现有一带负电的小球
从y轴上的P(0，L)点，在电场力作用下由静止开始运动，小球
发生碰撞，碰后两小球粘合在一起进入磁场，它们穿出磁场的位置恰好在O点．若
（即电荷量与质量之比）；
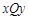是位于足够大的绝缘光滑水平桌面内的平面直角坐标系，虚线MN是∠
的角平分线．在MN的左侧区域，存在着沿
轴负方向、场强为E的匀强电场；在MN的右侧区域，存在着方向竖直向下、磁感应强度为B的匀强磁场，现有一带负电的小球
从y轴上的P(0，L)点，在电场力作用下由静止开始运动，小球
发生碰撞，碰后两小球粘合在一起进入磁场，它们穿出磁场的位置恰好在O点．若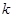
（即电荷量与质量之比）；