题目内容
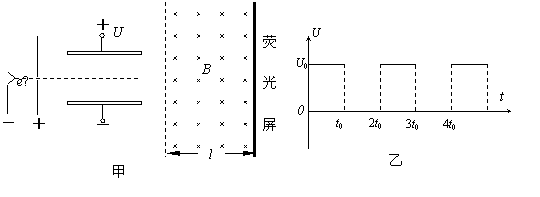
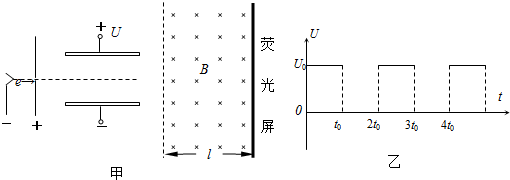
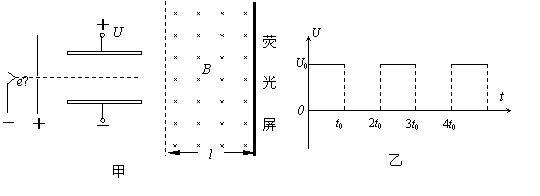
电子扩束装置由相邻的电子加速器、偏转电场和偏转磁场组成.偏转电场由两块水平平行放置的长为l相距为d的导体板组成,如图甲所示.大量电子(其重力不计,质量为m、电荷量为e)由静止开始,经加速电场加速后,连续不断地水平向右从两板正中间射入偏转电场.当两板不带电时,电子通过两板之间的时间均为2t,当在两板间加如图乙所示的周期为2t、最大值恒为U的电压时,所有电子均可射出偏转电场,并射入垂直纸面向里的匀强磁场,最后打在磁场右侧竖直放置的荧光屏上.磁场的水平宽度为s,竖直高度足够大.求:(1)加速电场的电压
(2)电子在离开偏转电场时的最大侧向位移;
(3)要使侧向位移最大的电子能垂直打在荧光屏上,匀强磁场的磁感应强度为多大?

【答案】分析:(1)当两板不带电时,电子在两板间做匀速直线运动,可求出电子的速度,再由动能定理研究加速过程,得到加速电场的电压;
(2)电子在t=0时刻进入偏转电场时,先做类平抛运动,后做匀速直线运动,要使电子的侧向位移最大,应让电子从0、2t、4t…等时刻进入偏转电场,由牛顿第二定律求出加速度,由运动学公式,运用运动的合成和分解法求出离开偏转电场时的侧向位移大小.
(3)设电子从偏转电场中射出时的偏向角为θ,要使侧向位移最大的电子能垂直打在荧光屏上,磁场中速度偏向角也为θ,由几何知识求出电子在磁场中运动半径,根据电子在电场中偏转情况求出θ的正弦,即可由R=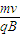 求出匀强磁场的磁感应强度.
求出匀强磁场的磁感应强度.
解答:解:(1)电子离开加速电场时的速度为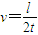
在加速电场中,由动能定理得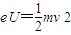
得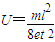
(2)要使电子的侧向位移最大,应让电子从0、2t、4t…等时刻进入偏转电场
由牛顿第二定律得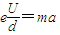
类平抛运动过程侧向位移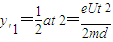 ,
,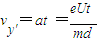
匀速直线运动侧向位移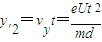
故最大侧向位移
(3)设电子从偏转电场中射出时的偏向角为θ,要电子垂直打在荧光屏上,则电子在磁场中运动半径应为: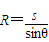
设电子从偏转电场中出来时的速度为v,垂直偏转极板的速度为vy,则电子从偏转电场中出来时的偏向角为: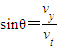
式中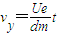
又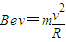
由上述四式可得: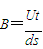
答:(1)加速电场的电压是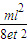 ;
;
(2)电子在离开偏转电场时的最大侧向位移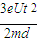 ;
;
(3)要使侧向位移最大的电子能垂直打在荧光屏上,匀强磁场的磁感应强度为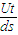 .
.
点评:本题的难点是分析带电粒子的运动情况,可通过画轨迹作速度图象分析什么时刻进入偏转电场的电子侧向最大.
(2)电子在t=0时刻进入偏转电场时,先做类平抛运动,后做匀速直线运动,要使电子的侧向位移最大,应让电子从0、2t、4t…等时刻进入偏转电场,由牛顿第二定律求出加速度,由运动学公式,运用运动的合成和分解法求出离开偏转电场时的侧向位移大小.
(3)设电子从偏转电场中射出时的偏向角为θ,要使侧向位移最大的电子能垂直打在荧光屏上,磁场中速度偏向角也为θ,由几何知识求出电子在磁场中运动半径,根据电子在电场中偏转情况求出θ的正弦,即可由R=
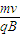 求出匀强磁场的磁感应强度.
求出匀强磁场的磁感应强度.解答:解:(1)电子离开加速电场时的速度为
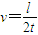
在加速电场中,由动能定理得
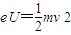
得
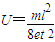
(2)要使电子的侧向位移最大,应让电子从0、2t、4t…等时刻进入偏转电场
由牛顿第二定律得
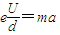
类平抛运动过程侧向位移
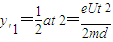 ,
,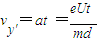
匀速直线运动侧向位移
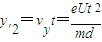
故最大侧向位移

(3)设电子从偏转电场中射出时的偏向角为θ,要电子垂直打在荧光屏上,则电子在磁场中运动半径应为:
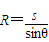
设电子从偏转电场中出来时的速度为v,垂直偏转极板的速度为vy,则电子从偏转电场中出来时的偏向角为:
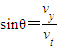
式中
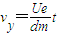
又
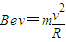
由上述四式可得:
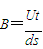
答:(1)加速电场的电压是
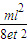 ;
;(2)电子在离开偏转电场时的最大侧向位移
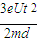 ;
;(3)要使侧向位移最大的电子能垂直打在荧光屏上,匀强磁场的磁感应强度为
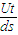 .
.点评:本题的难点是分析带电粒子的运动情况,可通过画轨迹作速度图象分析什么时刻进入偏转电场的电子侧向最大.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目