题目内容
在真空中速度为v=6.4×107 m/s的电子束连续地射入两平行极板之间(如图5-2-5所示).极板长度为L=8×10-2 m,间距为d=5×10-3 m.两极板不带电时,电子束将沿两极板之间的中线通过,在两极上加50 Hz的交变电压u=U0sinωt.如果所加电压的最大值U0超过某一值Uc,将开始出现以下现象:电子束有时能通过两极板;有时间断,不能通过.
图5-2-5
(1)求Uc的大小.
(2)求U0为何值时才能使通过的时间(Δt)通跟间断的时间(Δt)断之比为(Δt)通∶(Δt)断=2∶1.(电子质量m=0.91×10-30 kg,电子电荷量e=1.60×10-19 C)
思路分析:题中给出的是某种现象,解题时首先要把产生该现象的原因分析清楚.知道了为什么产生该现象,求解就容易了.各种物理现象都是在一定条件下发生的,如本题中电子能否穿越极板,决定于电压高低这一条件.会不会独立地分析题中所包含的条件,并能把它用数学式表达出来,这是区分能力高低的一个重要标志.分析和表达出题中所包含的条件,如本题中,注意到电子在电场中偏转距离与电压成正比,从而得到![]() ·
·![]() =
=![]() ,这也是解题的关键.
,这也是解题的关键.
解析:首先注意到电子通过两极板间的时间t=![]() =
=![]() s=1.25×10-9 s,交变电压的周期T=2π/ω=1/f=2×10-2 s,即t<<T.在电子通过两极板间的时间内,交变电压的数值变化极小,可以认为在这极短时间内电压不变,电子所受的电场力可以认为是恒力.
s=1.25×10-9 s,交变电压的周期T=2π/ω=1/f=2×10-2 s,即t<<T.在电子通过两极板间的时间内,交变电压的数值变化极小,可以认为在这极短时间内电压不变,电子所受的电场力可以认为是恒力.
(1)电子射入两极板间的匀强电场中后,沿v方向做匀速直线运动,沿垂直v的方向在恒定电场力作用下做初速度为零的匀加速直线运动.若两极板间电压为U,则场强E=![]() ,电场力F=
,电场力F=![]() ,加速度a=
,加速度a=![]() .电子在v方向和垂直v方向的运动方程为
.电子在v方向和垂直v方向的运动方程为
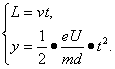 解得y=
解得y=![]() ·
·![]() .
.
如果y<d/2,则电子可以通过两极板;如果y>d/2,则电子将打到其中一个极板上,而不能通过两极板;如果y=d/2,则所对应的电压就是所要求的Uc的值,所以
![]() ·
·![]() =
=![]()
故Uc=![]()
=![]() V
V
=91 V.
(2)当两极板间电压U>Uc时,电子不能通过两极板;U<Uc时,电子能通过两极板.交变电压的正半周和负半周是对称的,我们只要分析正半周即可.

图5-2-6
题意要求(Δt)通∶(Δt)断=2∶1,为此,把正半周期的时间T/2分成3等份:T/6,T/3和T/2,如图5-2-6所示.在0—T/6和T/3—T/2的两段T/6时间内,电压U<Uc,电子能通过两极板.在T/6—T/3的一段T/6时间内,电压U>Uc,电子不能通过两极板.这就满足了(Δt)通∶(Δt)断=2∶1的要求.
所以U0·sinω![]() =Uc,即U0·sin
=Uc,即U0·sin![]() =Uc.
=Uc.
所以U0=![]() Uc=
Uc=![]() ×91 V=105 V.
×91 V=105 V.
答案:(1)91 V (2)105 V

 在真空中速度为v=6.4×107m/s的电子束连续射入两平行板间,如图所示,极板长度L=8.0×10-2m间距d=5.0×10-2m,两极板不带电时,电子将沿极板间的中线通过,在极板上加一个50Hz的交变电压u=U0sinωt,如果所加电压的最大值U0超过某值UC时,电子束将有时能通过两极板,有时间断而不能通过(电子电荷量e=1.6×10-19C,电子质量m=9.1×10-31kg).求:
在真空中速度为v=6.4×107m/s的电子束连续射入两平行板间,如图所示,极板长度L=8.0×10-2m间距d=5.0×10-2m,两极板不带电时,电子将沿极板间的中线通过,在极板上加一个50Hz的交变电压u=U0sinωt,如果所加电压的最大值U0超过某值UC时,电子束将有时能通过两极板,有时间断而不能通过(电子电荷量e=1.6×10-19C,电子质量m=9.1×10-31kg).求:

