题目内容
【题目】如图所示,质量为4kg的物体静止在水平面上,物体与水平面间的动摩擦因数为0.5。物体受到大小为30 N与水平方向成37°角斜向上的拉力F作用时,沿水平面做匀加速运动,(g取10 m/s2,sin37°=0.6,cos37°=0.8)求:
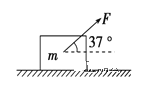
(1)物体加速度的大小.
(2)若人不改变推力F的大小,只把力的方向变为水平去推这个静止的箱子,推力作用时间t=4s后撤去,求箱子滑行的总位移为多大?
【答案】(1)3.25m/s2 (2)30m
【解析】
分析物体的受力情况,根据牛顿第二定律,运用正交分解法求得加速度a的大小;由牛顿第二定律可求得前4s的加速度,由速度公式求得4s末时的速度,由位移公式可求得前4s内的位移;同理求得撤去F后的加速度及位移;即可求得总位移.
(1)选取物体为研究对象,对其受力分析,如图所示:
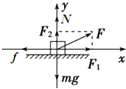
由牛顿第二定律得,水平方向:Fcos37°-f=ma
竖直方向:N+Fsin37°=mg
又f=μN
联立解得:a=3.25m/s2.
(2)当力改为水平方向时,由牛顿第二定律得,水平方向:F-f1=ma1
竖直方向:N1=mg
又f1=μN1
联立解得:a1=2.5m/s2
4s末的速度为:v1=a1t1=10m/s
前4s内的位移:![]()
撤去F后:-f2=ma2
解得:a2=5m/s2
箱子还能滑行:![]() .
.
所以箱子通过的总位移:x=x1+x2=30m

 名校课堂系列答案
名校课堂系列答案【题目】如图甲所示是某同学探究加速度与力的关系的实验装置.他在气垫导轨上安装了一个光电门B,滑块上固定一遮光条,滑块用细线绕过气垫导轨左端的定滑轮与力传感器相连,力传感器可直接测出绳中拉力,传感器下方悬挂钩码,每次滑块都从A处由静止释放。气垫导轨摩擦阻力很小可忽略不计,由于遮光条的宽度很小,可认为遮光条通过光电门时速度不变。


(1)该同学用游标卡尺测量遮光条的宽度d,如图乙所示,则d= mm.
(2)实验时,该同学用游标卡尺测量遮光条的宽度d,将滑块从A位置由静止释放,测量遮光条到光电门的距离L,若要得到滑块的加速度,还需由数字计时器读出遮光条通过光电门B的 ;
(3)下列不必要的一项实验要求是( )。
A.应使滑块质量远大于钩码和力传感器的总质量 |
B.应使A位置与光电门间的距离适当大些 |
C.应将气垫导轨调节水平 |
D.应使细线与气垫导轨平行 |
(4)改变钩码质量,测出对应的力传感器的示数F,已知滑块总质量为M,用(2)问中已测物理量和已给物理量写出M和F间的关系表达式F= 。