题目内容
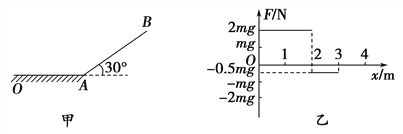
【题目】如下图所示，在倾角为30°的光滑斜面体上，一劲度系数为k＝200N/m的轻质弹簧一端连接固定挡板C，另一端连接一质量为m＝4kg的物体A，一轻细绳通过定滑轮，一端系在物体A上，另一端与质量也为m的物体B相连，细绳与斜面平行，斜面足够长，用手托住物体B使细绳刚好没有拉力，然后由静止释放，物体B不会碰到地面，重力加速度g＝10m/s2，求：
(1)释放B的瞬间，弹簧的压缩量
和A与B的共同加速度；
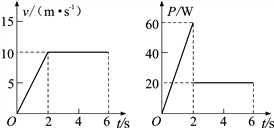
(2)物体A的最大速度大小vm；
(3)将物体B改换成物体C，其他条件不变， A向上只能运动到弹簧原长，求物体C的质量M
【答案】（1）5m/s2 ；(2) 1 m/s；（3）1kg
【解析】
（1）由胡克定律，得：
设绳子拉力T,由牛顿第二定律，得：
解得
（2）当A、B物体的加速度为0时，速度最大，设此时拉力
,弹簧伸长量
，则
由平衡条件，得: 
解得
由开始运动到达到最大速度过程，弹性势能不变，由能量守恒定律，得
解得
（3）弹簧恢复原长时,弹簧弹性势能减少： 
由能量守恒定律，得：
解得 M=1kg
【题目】为了验证机械能守恒定律，小明设计了如图甲所示的实验，将一长为
的气垫导轨固定在一平台上，将一宽度为
的遮光条固定在滑块上，经测量可知遮光条和滑块的总质量为
，气垫导轨的顶端到平台的高度为
，将一质量为
的钩码通过质量不计的细线与滑块相连，并跨过图甲中的摩擦不计的定滑轮；将一光电门固定在气垫导轨上，光电门到顶端的距离为
。将滑块由气垫导轨的顶端静止释放，滑块沿气垫导轨下滑，经测量遮光条的挡光时间为
，重力加速度用
表示。请回答下列问题：
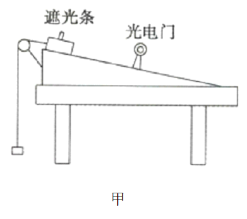
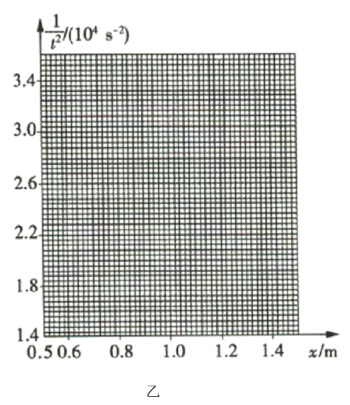
(1)上述过程中滑块和钩码的重力势能减少了_________________，滑块和钩码的动能增加了_________________，如果在误差允许的范围内系统的机械能守恒，则
关于的表达式为_________________；
(2)小明进行了多次操作，并将每次测量的实验数据记录在表中：
1 | 2 | 3 | 4 | 5 | |
| 0.600 | 0.800 | 1.000 | 1.200 | 1.400 |
| 1.48 | 1.95 | 2.41 | 2.92 | 3.39 |
建立如图乙所示的坐标系，请根据图表中的数据作出相应的函数图线_________________，并由图像求出该直线斜率的大小为_________________ 
。（保留3位有效数字）
