��Ŀ����
����Ŀ����ͼ��ʾ���ռ��д���һˮƽ�������ǿ�糡��һˮƽ�������ǿ�ų����ҵ糡����ʹų��������ֱ���ڵ�ų������Ŀռ�����һ�㹻���Ĺ̶��ֲھ�Ե�ˣ���糡�������60�����Ҵ�����ֱƽ���ڡ�һ����Ϊm�������Ϊ��q��q![]() 0����С�����ھ�Ե���ϣ���С��һ�ظ����µij��ٶ�v0��С��ǡ���������˶�����������ֲ��䡣��֪�Ÿ�Ӧǿ�ȴ�СΪB���糡ǿ�ȴ�СΪE��
0����С�����ھ�Ե���ϣ���С��һ�ظ����µij��ٶ�v0��С��ǡ���������˶�����������ֲ��䡣��֪�Ÿ�Ӧǿ�ȴ�СΪB���糡ǿ�ȴ�СΪE��![]() ��������˵���в���ȷ���ǣ� ��
��������˵���в���ȷ���ǣ� ��

A.С��ij��ٶ�v0��![]()
B.��С��ij��ٶ�Ϊ![]() ��С�������ٶȲ�������ļ����˶������ֹͣ
��С�������ٶȲ�������ļ����˶������ֹͣ
C.��С��ij��ٶ�Ϊ![]() ��С�������ٶȲ�������ļ����˶������ֹͣ
��С�������ٶȲ�������ļ����˶������ֹͣ
D.��С��ij��ٶ�Ϊ![]() �����˶��п˷�Ħ��������Ϊ
�����˶��п˷�Ħ��������Ϊ![]()
���𰸡�B
��������
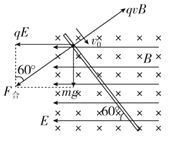
A.��С���������������ͼ��ʾ���糡���Ĵ�СF��qE��![]() mg�����������ķ�����ֱ���£��糡���ķ���ˮƽ�����ߴ�ֱ�����ߵĺ���F����2mg��������˵ķ���ֱ�������������ķ���Ҳ���ٶȵķ���ֱ���������ĺ��������������Ե�С��������ֱ���˶�ʱ�������ܴ���Ħ��������˶�С��û��֧���������ã���qv0B��2mg��v0��
mg�����������ķ�����ֱ���£��糡���ķ���ˮƽ�����ߴ�ֱ�����ߵĺ���F����2mg��������˵ķ���ֱ�������������ķ���Ҳ���ٶȵķ���ֱ���������ĺ��������������Ե�С��������ֱ���˶�ʱ�������ܴ���Ħ��������˶�С��û��֧���������ã���qv0B��2mg��v0��![]() ����A��ȷ���������⣻
����A��ȷ���������⣻
B.��С��ij��ٶ�Ϊ![]() ����ʱ��������F����qvB��3mg
����ʱ��������F����qvB��3mg![]() F�����ڴ�ֱ�ڸ˵ķ����ϣ�С���ܵ��˵�֧����������Ħ����f����FN��С���������˶��������ٶȵļ�С������������С����֧������С��Ħ����Ҳ��С��С�������ٶȲ��ϼ�С�ļ����˶�������ٶȼ�С��
F�����ڴ�ֱ�ڸ˵ķ����ϣ�С���ܵ��˵�֧����������Ħ����f����FN��С���������˶��������ٶȵļ�С������������С����֧������С��Ħ����Ҳ��С��С�������ٶȲ��ϼ�С�ļ����˶�������ٶȼ�С��![]() ʱ��FN��0��f��0��С��ʼ������ֱ���˶�����B���������⣻
ʱ��FN��0��f��0��С��ʼ������ֱ���˶�����B���������⣻
C.��С��ij��ٶ�Ϊv=![]() ����ʱ��������F����qvB��mg
����ʱ��������F����qvB��mg![]() F�����ڴ�ֱ�ڸ˵ķ����ϣ�С���ܵ��˵�֧����������Ħ����f����FN��С���������˶��������ٶȵļ�С������������С����֧����������Ħ����������С��ļ��ٶ���������С�������ٶȲ�������ļ����˶������ֹͣ����C��ȷ���������⣻
F�����ڴ�ֱ�ڸ˵ķ����ϣ�С���ܵ��˵�֧����������Ħ����f����FN��С���������˶��������ٶȵļ�С������������С����֧����������Ħ����������С��ļ��ٶ���������С�������ٶȲ�������ļ����˶������ֹͣ����C��ȷ���������⣻
D.��C��ķ�����֪�˶��п˷�Ħ���������Ĺ�����С���ܵļ�С���������͵糡���ĺ���������������
Wf��![]() mv��2��
mv��2��![]()
��D��ȷ���������⡣
��ѡB��