题目内容
如图，a是静止在地球赤道上的物体，b、c是两颗人造地球卫星，其中c是地球的同步卫星，a、b、c在同一平面内沿不同的轨道绕地心做匀速圆周运动，三者绕行方向相同（为图示顺时针方向），已知Rb=| Rc |
| 4 |
分析：根据万有引力提供向心力知，轨道半径越大，周期越大，则角速度越小，所以经过相同的时间，可以比较出三卫星转过的角度，而同步卫星又与地球保持相对静止．
解答：解：同步卫星又与地球保持相对静止，所以物体a、卫星c的角速度相同．所以C始终在a的正上方．
根据万有引力提供向心力知，轨道半径越大，周期越大，则角速度越小，所以卫星b的角速度是c的角速度4倍．
所以经过6小时C回到原位置．
故选C．
根据万有引力提供向心力知，轨道半径越大，周期越大，则角速度越小，所以卫星b的角速度是c的角速度4倍．
所以经过6小时C回到原位置．
故选C．
点评：解决本题的关键掌握万有引力提供向心力，知道周期与轨道半径的关系以及知道同步卫星的特点．
练习册系列答案
科学实验活动册系列答案
相关题目
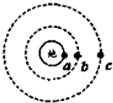如图，a是静止在地球赤道上的物体，b、c是两颗人造地球卫星，其中c是地球的同步卫星，a、b、c在同一平面内沿不同的轨道绕地心做匀速圆周运动，三者绕行方向相同（为图示顺时针方向），已知Rb＜Rc．若在某一时刻，它们正好运行到同一条直线上，如图所示．那么再经过6小时，物体a、卫星b、c的位置可能是（ ）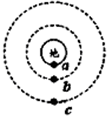
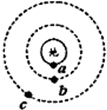
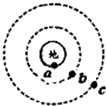
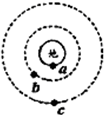
．若在某一时刻，它们正好运行到同一条直线上，如图甲所示．那么再经过6小时，物体a、卫星b、c的位置可能是图中的（ ）
