题目内容
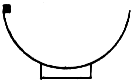 一个质量为m的小铁块沿半径为R的固定半圆轨道上端边缘由静止下滑,当滑到半球底部时,半圆轨道底部所受压力为铁块重力的1.8倍,则此下滑过程中( )
一个质量为m的小铁块沿半径为R的固定半圆轨道上端边缘由静止下滑,当滑到半球底部时,半圆轨道底部所受压力为铁块重力的1.8倍,则此下滑过程中( )| A、铁块机械能守恒 | B、铁块动能的增加为0.4mgR | C、铁块损失的机械能为0.6mgR | D、铁块滑到最低点时重力的功率为mg |
分析:当铁块滑到半球底部时,半圆轨道底部所受压力为铁块重力的1.5倍,根据牛顿第二定律和向心力公式可以求出此时铁块的速度;分析铁块下滑过程中,是否只有重力做功,判断机械能是否守恒;损失的机械能等于初末机械能之差.重力的功率等于重力与竖直分速度大小的乘积.
解答:解:
A、铁块滑到半球底部时,半圆轨道底部所受压力为铁块重力的1.8倍,对铁块,根据牛顿第二定律,有
N-mg=m
①
因铁块对轨道的压力大小等于轨道对铁块的支持力大小,根据题意,有
N=1.8mg ②
联立①②得:v=
若铁块下滑过程机械能守恒,设铁块滑到轨道底端时的速度大小为V,则得:
mgR=
mV2 ③
由③式解得:V=
因V>v,所以铁块的机械能不守恒,故A错误.
B、铁块增加的动能为△Ek=
mv2=0.4mgR,故B正确.
C、铁块损失的机械能为:△E=mgR-
mv2=0.6mgR,故C正确.
D、铁块滑到最低点时速度水平向右,没有竖直分速度,所以此时重力的瞬时功率为0,故D错误.
故选:BC.
A、铁块滑到半球底部时,半圆轨道底部所受压力为铁块重力的1.8倍,对铁块,根据牛顿第二定律,有
N-mg=m
| v2 |
| R |
因铁块对轨道的压力大小等于轨道对铁块的支持力大小,根据题意,有
N=1.8mg ②
联立①②得:v=
| 0.8gR |
若铁块下滑过程机械能守恒,设铁块滑到轨道底端时的速度大小为V,则得:
mgR=
| 1 |
| 2 |
由③式解得:V=
| 2gR |
因V>v,所以铁块的机械能不守恒,故A错误.
B、铁块增加的动能为△Ek=
| 1 |
| 2 |
C、铁块损失的机械能为:△E=mgR-
| 1 |
| 2 |
D、铁块滑到最低点时速度水平向右,没有竖直分速度,所以此时重力的瞬时功率为0,故D错误.
故选:BC.
点评:本题是机械能守恒、牛顿第二定律和功能关系的综合应用.对于机械能的损失,也可以根据损失失的机械能等于克服摩擦力做的功,由动能定理求解.

练习册系列答案
相关题目
 (2010?盐池县模拟)一个质量为m的小铁块沿半径为R的固定半圆轨道上端边缘由静止下滑,当滑到半球底部时,半圆轨道底部所受压力为铁块重力的1.8倍,则此下滑过程中铁块损失的机械能为( )
(2010?盐池县模拟)一个质量为m的小铁块沿半径为R的固定半圆轨道上端边缘由静止下滑,当滑到半球底部时,半圆轨道底部所受压力为铁块重力的1.8倍,则此下滑过程中铁块损失的机械能为( ) 质量为M的小车,静止在光滑的水平面上,现有一个质量为m的小铁块,以初速度v0从左端滑上小车,如图所示,铁块与小车间的动摩擦因数为μ,求:
质量为M的小车,静止在光滑的水平面上,现有一个质量为m的小铁块,以初速度v0从左端滑上小车,如图所示,铁块与小车间的动摩擦因数为μ,求: 一个质量为m的小铁块沿半径为R 的固定半圆轨道上边缘由静止滑下,到半圆底部时,轨道所受压力为铁块重力的1.5倍,则此过程中克服摩擦力所做的功为( )
一个质量为m的小铁块沿半径为R 的固定半圆轨道上边缘由静止滑下,到半圆底部时,轨道所受压力为铁块重力的1.5倍,则此过程中克服摩擦力所做的功为( ) 如图所示,传送带以速度v沿顺时针方向传动,把一个质量为m的小铁块A轻轻放在传动带的左端,小铁块与传送带的动摩擦因数为μ,以下说法正确的是( )
如图所示,传送带以速度v沿顺时针方向传动,把一个质量为m的小铁块A轻轻放在传动带的左端,小铁块与传送带的动摩擦因数为μ,以下说法正确的是( ) 一个质量为m的小铁块沿半径为R的固定半圆轨道上边缘由静止滑下,到半圆底部时,小铁块所受向心力为铁块重力的1.5倍,则此过程中铁块损失的机械能为( )
一个质量为m的小铁块沿半径为R的固定半圆轨道上边缘由静止滑下,到半圆底部时,小铁块所受向心力为铁块重力的1.5倍,则此过程中铁块损失的机械能为( )