题目内容
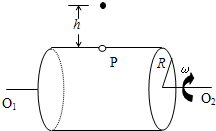 如图所示,一个水平放置的圆桶绕水平轴O1O2匀速转动,桶的半径R=2m,桶壁很薄,壁上有一小圆孔P,当圆孔运动到桶的正上方时,在孔的正上方h=3.2m处有一个小球由静止开始下落,已知圆孔的半径略大于小球的半径.试求:要使小球在整个下落过程中都不与桶壁碰撞,圆桶转动的角速度的所有可能值.
如图所示,一个水平放置的圆桶绕水平轴O1O2匀速转动,桶的半径R=2m,桶壁很薄,壁上有一小圆孔P,当圆孔运动到桶的正上方时,在孔的正上方h=3.2m处有一个小球由静止开始下落,已知圆孔的半径略大于小球的半径.试求:要使小球在整个下落过程中都不与桶壁碰撞,圆桶转动的角速度的所有可能值.分析:小球若能从圆孔中进去还正好从圆孔中出来,就不会跟圆筒相撞,否则就会相撞,设小球下落h所用时间t1,经过圆桶所用时间为t2,求出这两段时间,再求出圆筒的角速度的可能值.
解答:解:设小球下落h所用时间t1,经过圆桶所用时间为t2,则h=
gt2
解得t1=0.8 s
h+2R=
g(t1+t2)2
解得t2=0.4 s
设圆桶的运动周期为T,故有:
nT=t1(n=1,2,3,…)
(m-
)T=t2 (m=1,2,3,…)
解得:T=
(n=1,2,3,…)
且T=
(m=1,2,3,…)
故T=
(m=1,2,3,…)
角速度为:ω=
=2.5π(2m-1)(m=1,2,3,…)
答:要使小球在整个下落过程中都不与桶壁碰撞,圆桶转动的角速度的可能值为:ω=
=2.5π(2m-1)(m=1,2,3,…).
| 1 |
| 2 |
解得t1=0.8 s
h+2R=
| 1 |
| 2 |
解得t2=0.4 s
设圆桶的运动周期为T,故有:
nT=t1(n=1,2,3,…)
(m-
| 1 |
| 2 |
解得:T=
| 0.8 |
| n |
且T=
| 0.8 |
| 2m-1 |
故T=
| 0.8 |
| 2m-1 |
角速度为:ω=
| 2π |
| T |
答:要使小球在整个下落过程中都不与桶壁碰撞,圆桶转动的角速度的可能值为:ω=
| 2π |
| T |
点评:本题是自由落体运动和圆周运动相结合的题目,比较有新意,要抓住小球运动时间与圆筒的周期之间的关系求解,难度适中.

练习册系列答案
相关题目
 如图所示,半径为R的光滑圆轨道竖直放置,长为2R的轻质杆两端各固定一个可视为质点的小球A、B,把轻杆水平放入圆形轨道内,若m,2m,m0,m,重力加速度为g,现由静止释放两球,当轻杆到达竖直位置时,求:
如图所示,半径为R的光滑圆轨道竖直放置,长为2R的轻质杆两端各固定一个可视为质点的小球A、B,把轻杆水平放入圆形轨道内,若m,2m,m0,m,重力加速度为g,现由静止释放两球,当轻杆到达竖直位置时,求: 如图所示,两根无阻导轨与水平面成θ=370角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=lΩ电动势未知的电源两极相连,杆与导轨问最大静摩擦力fm=15N.当导轨间有竖直向上、磁感强度为B=2T的匀强磁场时,杆与导轨间刚好无摩擦力.求:
如图所示,两根无阻导轨与水平面成θ=370角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=lΩ电动势未知的电源两极相连,杆与导轨问最大静摩擦力fm=15N.当导轨间有竖直向上、磁感强度为B=2T的匀强磁场时,杆与导轨间刚好无摩擦力.求: 如图所示,两根无电阻导轨与水平面成θ=37°角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=1Ω电动势未知的电源两极相连,杆与导轨间最大静摩擦力fm=1.5N.当导轨间有竖直向上、磁感应强度为B=2T的匀强磁场时,杆与导轨间刚好无摩擦力.求:
如图所示,两根无电阻导轨与水平面成θ=37°角放置,两导轨间距离为d=0.5m,在导轨上垂直于导轨水平放一根质量m=0.2kg、长度略大于d、电阻R=4Ω的均匀金属杆,导轨下端与一个内阻r=1Ω电动势未知的电源两极相连,杆与导轨间最大静摩擦力fm=1.5N.当导轨间有竖直向上、磁感应强度为B=2T的匀强磁场时,杆与导轨间刚好无摩擦力.求: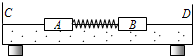 气垫导轨是常用的一种实验仪器,它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦.我们可以用带竖直挡板C和D的气垫导轨和滑块A和B验证动量守恒定律,实验装置如图所示,采用的实验步骤如下:
气垫导轨是常用的一种实验仪器,它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦.我们可以用带竖直挡板C和D的气垫导轨和滑块A和B验证动量守恒定律,实验装置如图所示,采用的实验步骤如下: