题目内容
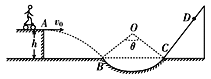
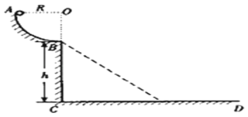
【题目】如图所示,轨道ABCD的AB段为一半径R=1m的![]() 圆形轨道,BC段为高为h=5m的竖直轨道,CD段为水平轨道.一质量为0.5kg的小球由A点运动到B点,离开B点做平抛运动,由于存在摩擦力的缘故小球在圆弧轨道上的速度大小始终为2m/s.(g取10m/s2),(取π=3).求:
圆形轨道,BC段为高为h=5m的竖直轨道,CD段为水平轨道.一质量为0.5kg的小球由A点运动到B点,离开B点做平抛运动,由于存在摩擦力的缘故小球在圆弧轨道上的速度大小始终为2m/s.(g取10m/s2),(取π=3).求:
(1)小球从A点运动到B点的时间和此时小球对圆形轨道的压力;
(2)如果在BCD轨道上放置一个倾角θ=37°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上时距B点的距离,如果不能,求落在CD面上的位置到C点的距离.
【答案】(1)0.75s;7N(2)0.75m
【解析】
(1)小球从A点运动到B的时间为
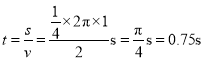
在B点,由牛顿第二定律有:
FN-mg=![]()
解得
FN=7N
由牛顿第三定律知小球对轨道的压力
FN′=FN=7N
方向:竖直向下
(2)当没有斜面时小球落地的时间为
![]()
假设小球能够落在斜面上,设时间为t′,则
tanθ= ![]()
可得
t′=0.3s
因为t′<t,所以小球能够落在斜面上;
平抛运动的水平位移为
x=vt′=2×0.3m=0.6m
落在CD面上的位置到B点的距离
s=![]() =
=![]() =0.75m
=0.75m
即能落到斜面上,落在CD面上的位置到B点的距离是0.75m.

练习册系列答案
相关题目