题目内容
一只小船在静水中的速度为5m/s,河水流速为3 m/s,河宽为500 m,求下列各情况中,船头的指向与河岸的夹角和过河时间.
?(1)船要以最小位移过河;
?(2)船要以最短时间过河;
?(3)船要到达正对岸下游100m处;
?(4)若船在静水中的速度是![]() m/s,则船要以最小位移过河,那么船头航向与河岸成的夹角θ和过河位移s分别是多少?
m/s,则船要以最小位移过河,那么船头航向与河岸成的夹角θ和过河位移s分别是多少?
(1)53°,125s (2)90°,100s?(3)74.4°,104 s?(4)46.8°,500![]() m
m
解析:
小船过河同时参与划行运动和随水流运动,设船头航向与河岸成α角,如图甲所示,

?(1)要使船以最小位移过河,船应在B点靠岸.v划cosα=v水,cosα=![]() =
=![]() ,α=53°,d=v划sinα·t,t=
,α=53°,d=v划sinα·t,t=![]() =
=![]() =125s.(2)船要以最短时间过河,由t=
=125s.(2)船要以最短时间过河,由t=![]() 得sinα=1时,t最小,则α=90°,且tmin=500/5s=100s.(3)船要在对岸下游100m靠岸,则(v水-v划cosα)t=100,v划sinαt=500,即26cos2α+30cosα-10=0, cosα=7/26, sinα=25/26,则α=arccos
得sinα=1时,t最小,则α=90°,且tmin=500/5s=100s.(3)船要在对岸下游100m靠岸,则(v水-v划cosα)t=100,v划sinαt=500,即26cos2α+30cosα-10=0, cosα=7/26, sinα=25/26,则α=arccos![]() -74.4°,t=104s.(4)若船的划行速度为v水=
-74.4°,t=104s.(4)若船的划行速度为v水=![]() m/s,比水流速度小,所以船不可能垂直河岸到达对岸,一定在对岸下游靠岸.要使船以最小位移过河,必须使如图乙所示中的α最大,根据正弦定理有
m/s,比水流速度小,所以船不可能垂直河岸到达对岸,一定在对岸下游靠岸.要使船以最小位移过河,必须使如图乙所示中的α最大,根据正弦定理有![]() ,所以sinα=v划sinβ/v水,当sinβ=1,即β=90°时,α最大,这时过河位移最小为smin,且sinθ=cosα=
,所以sinα=v划sinβ/v水,当sinβ=1,即β=90°时,α最大,这时过河位移最小为smin,且sinθ=cosα=![]() ,所以θ=arcsin
,所以θ=arcsin![]() =46.8°,由正交分解有L=v划tcosα,smin=
=46.8°,由正交分解有L=v划tcosα,smin=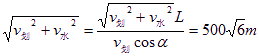 .
.

练习册系列答案
相关题目