题目内容
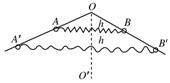
如右图所示,竖直平面内两根光滑细杆所构成的角∠AOB被铅垂线OO′平分,∠AOB=120°.两个质量均为m的小环P、Q通过水平轻弹簧的作用静止在A、B两处,A、B连线与OO′垂直,连线与O点的距离为h,弹簧原长为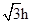 .现在两小环沿杆向下移动至A′B′,使其在竖直方向上均下移h距离,同时释放两环.整个过程未超出弹簧的弹性限度,重力加速度为g,试求:
.现在两小环沿杆向下移动至A′B′,使其在竖直方向上均下移h距离,同时释放两环.整个过程未超出弹簧的弹性限度,重力加速度为g,试求:
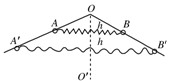
(1)弹簧的劲度系数;
(2)释放瞬间两环加速度的大小.
【答案】
(1) 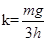 (2)g
(2)g
【解析】
试题分析:(1)在A、B处,弹簧处于伸长状态,伸长量
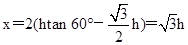
由小环P(或Q)受力平衡可知:
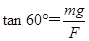
根据胡克定律知F=kx.
解之得
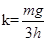 .
.
(2)在A′、B′处,弹簧伸长量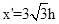
此时弹簧弹力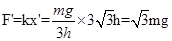 .
.
由牛顿第二定律知,释放瞬间 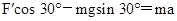
解得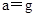 .
.
考点:牛顿第二定律;力的合成与分解的运用;胡克定律.
点评:本题根据先后对 小环受力分析,运用共点力平衡条件、牛顿第二定律并结合胡克定律列式分析求解.

练习册系列答案
相关题目
 甲、乙、丙三个小球分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平初速度v0做平抛运动,乙以水平初速度v0沿光滑水平面向右做匀速直线运动,丙做自由落体运动,则下列说法正确的是( )
甲、乙、丙三个小球分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平初速度v0做平抛运动,乙以水平初速度v0沿光滑水平面向右做匀速直线运动,丙做自由落体运动,则下列说法正确的是( )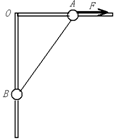 如图所示,竖直平面内放一直角杆,杆的水平部分粗糙,竖直部分光滑,两部分各套有质量分别为mA=2.0kg和mB=1.0kg的小球A和B,A球与水平杆间动摩擦因数μ=0.20,A,B间用不可伸长的轻绳相连,图示位置处OA=1.5m,OB=2.0m,g取10m/s2.(1)若用水平力F沿杆向右拉A,使A由图示位置向右极缓慢地移动0.5m,则该过程中拉力F1作了多少功?
如图所示,竖直平面内放一直角杆,杆的水平部分粗糙,竖直部分光滑,两部分各套有质量分别为mA=2.0kg和mB=1.0kg的小球A和B,A球与水平杆间动摩擦因数μ=0.20,A,B间用不可伸长的轻绳相连,图示位置处OA=1.5m,OB=2.0m,g取10m/s2.(1)若用水平力F沿杆向右拉A,使A由图示位置向右极缓慢地移动0.5m,则该过程中拉力F1作了多少功?