题目内容
【题目】如图所示,在竖直平面内半径为R的光滑圆形绝缘轨道的内壁,有质量分别为m和2m的A、B两个小球用长为R的绝缘细杆连接在一起,A球不带电,B球所带的电荷量为-q(q>0)。整个装置处在竖直向下的匀强电场中。开始时A球处在与圆心等高的位置,现由静止释放,B球刚好能到达轨道右侧与圆心等高的位置C。求:
(1)匀强电场电场强度的大小E;
(2)当B小球运动到最低点P时,两小球的动能分别是多少;
(3)两小球在运动过程中最大速度的大小。

【答案】(1) ![]() (2)
(2) 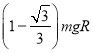 (2)
(2) ![]()
【解析】(1)B刚好到达C的过程中,系统转过的角度为120°,与水平方向的夹角为60°.由动能定理可得:
![]()
得: ![]()
(2)AB在运动的过程中,速度大小始终相等,则![]()
在运动到p点的过程中,由动能定理可得: ![]()
联立解得: 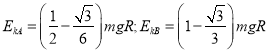 .
.
(3)设OA转过的角度为![]() 时,两球有最大速度,则由动能定理可得:
时,两球有最大速度,则由动能定理可得:
![]()
整理得: 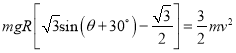
看见,当![]() 时,有最大速度,最大速度为
时,有最大速度,最大速度为
![]()

练习册系列答案
相关题目