题目内容
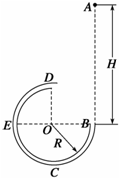 如图所示,四分之三周长圆管的半径R=0.4m,管口B和圆心O在同一水平面上,D是圆管的最高点,其中半圆周BE段存在摩擦,BC和CE段动摩擦因数相同,ED段光滑;质量m=0.5kg、直径稍小于圆管内径的小球从距B正上方高H=2.5m的A处自由下落,到达圆管最低点C时的速率为6m/s,并继续运动直到圆管的最高点D飞出,恰能再次进入圆管,假定小球再次进入圆筒时不计碰撞能量损失,取重力加速度g=10m/s2,求
如图所示,四分之三周长圆管的半径R=0.4m,管口B和圆心O在同一水平面上,D是圆管的最高点,其中半圆周BE段存在摩擦,BC和CE段动摩擦因数相同,ED段光滑;质量m=0.5kg、直径稍小于圆管内径的小球从距B正上方高H=2.5m的A处自由下落,到达圆管最低点C时的速率为6m/s,并继续运动直到圆管的最高点D飞出,恰能再次进入圆管,假定小球再次进入圆筒时不计碰撞能量损失,取重力加速度g=10m/s2,求(1)小球飞离D点时的速度.
(2)小球从B点到D点过程中克服摩擦所做的功.
(3)小球再次进入圆管后,能否越过C点?请分析说明理由.
分析:(1)小球从最高点D飞出做平抛运动,由水平距离和竖直距离求出小球飞离D点时的速度.
(2)根据动能定理求出小球从B点到D点过程中克服摩擦所做的功.
(3)应用动能定理求出小球第二次经过C点的速度,如果经过C点的速度大于零,则能过C点,如果小于零,则不能过C点.
(2)根据动能定理求出小球从B点到D点过程中克服摩擦所做的功.
(3)应用动能定理求出小球第二次经过C点的速度,如果经过C点的速度大于零,则能过C点,如果小于零,则不能过C点.
解答:解:(1)小球飞离D点后做平抛运动,
在水平方向:R=vDt,竖直方向:R=
gt2,
解得:vD=
m/s;
(2)小球从A到D过程中,由动能定理得:
mg(H-R)-Wf1=
mvD2-0,解得:Wf1=10J;
(3)小球从C到D过程中,由动能定理得:
-2mgR-Wf2=
mvD2-
mvC2,解得:Wf2=4.5J,
小球从A到C过程中,由动能定理得:
mg(H+R)-Wf3=
mvC2-0,解得:Wf3=5.5J;
小球再次从D到C的过程中,由动能定理得:
-2mgR-Wf4=
mvC2-
mvD2,
解得:Wf4=4.5J-
mvC2,
Wf4<Wf2=4.5J,vC′>0,小球能过C点.
答:(1)小球飞离D点时的速度为
m/s.
(2)小球从B点到D点过程中克服摩擦所做的功为10J.
(3)小球再次进入圆管后,能越过C点,因为到达C点时速度大于零.
在水平方向:R=vDt,竖直方向:R=
| 1 |
| 2 |
解得:vD=
| 2 |
(2)小球从A到D过程中,由动能定理得:
mg(H-R)-Wf1=
| 1 |
| 2 |
(3)小球从C到D过程中,由动能定理得:
-2mgR-Wf2=
| 1 |
| 2 |
| 1 |
| 2 |
小球从A到C过程中,由动能定理得:
mg(H+R)-Wf3=
| 1 |
| 2 |
小球再次从D到C的过程中,由动能定理得:
-2mgR-Wf4=
| 1 |
| 2 |
| 1 |
| 2 |
解得:Wf4=4.5J-
| 1 |
| 2 |
Wf4<Wf2=4.5J,vC′>0,小球能过C点.
答:(1)小球飞离D点时的速度为
| 2 |
(2)小球从B点到D点过程中克服摩擦所做的功为10J.
(3)小球再次进入圆管后,能越过C点,因为到达C点时速度大于零.
点评:本题是动能定理和向心力知识的综合应用,这类问题常常涉及到临界条件.第(3)问中用动能定理求变力的功也是常用方法.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
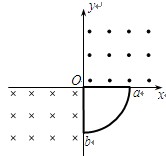
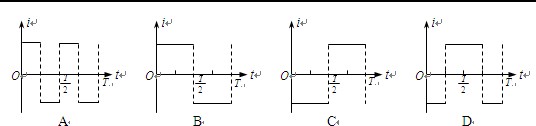
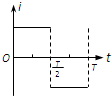
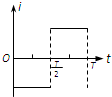
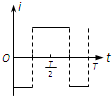
 如图所示,xOy坐标系第一象限内有垂直纸面向外的匀强磁场,第三象限内有垂直纸面向里的匀强磁场,磁感强度大小均为B,第二、四象限内没有磁场.一个围成四分之一圆弧形的导体环Oab,其圆心在原点O,开始时导体环在第四象限,且导体环两边oa、ob恰好分别与x轴、y轴重合,从t=0时刻开始导体环绕O点在xOy坐标平面内逆时针匀速转动.规定逆时针方向为电流的正方向,在导体环转动一周的过程中,下列能正确表示环内感应电流i随时间t变化的图象是( )
如图所示,xOy坐标系第一象限内有垂直纸面向外的匀强磁场,第三象限内有垂直纸面向里的匀强磁场,磁感强度大小均为B,第二、四象限内没有磁场.一个围成四分之一圆弧形的导体环Oab,其圆心在原点O,开始时导体环在第四象限,且导体环两边oa、ob恰好分别与x轴、y轴重合,从t=0时刻开始导体环绕O点在xOy坐标平面内逆时针匀速转动.规定逆时针方向为电流的正方向,在导体环转动一周的过程中,下列能正确表示环内感应电流i随时间t变化的图象是( )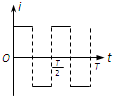
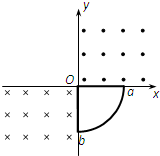
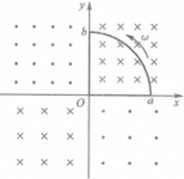 在平面直角坐标系的四个象限中存在着垂直纸面的匀强磁场,各象限中的磁场方向如图所示,第一、二象限中的磁感应强度:大小均为2B,第三、四象限中的磁感应强度大小均为B,一个四分之一圆形闭合导体线框Oab,从第一象限中的图示位置开始绕坐标原点O沿逆时针方向以恒定角速度ω在Oxy平面内匀速旋转一周,若线框中的电流取逆时针方向为正,则在此过程中线框中电流i随时间t的变化关系正确的是( )
在平面直角坐标系的四个象限中存在着垂直纸面的匀强磁场,各象限中的磁场方向如图所示,第一、二象限中的磁感应强度:大小均为2B,第三、四象限中的磁感应强度大小均为B,一个四分之一圆形闭合导体线框Oab,从第一象限中的图示位置开始绕坐标原点O沿逆时针方向以恒定角速度ω在Oxy平面内匀速旋转一周,若线框中的电流取逆时针方向为正,则在此过程中线框中电流i随时间t的变化关系正确的是( )