题目内容
用电阻率为ρ、横截面积为S的薄金属条制成边长为L的闭合正方形框abb′a′。金属方框水平放在磁极的狭缝间,方框平面与磁场方向平行,如图1、2所示。设匀强磁场仅存在于相对磁极之间,其他地方的磁场忽略不计。可认为方框的aa′边和bb′边都处在磁极间,极间磁感应强度大小为B。当t=0时,方框从静止开始释放,与底面碰撞后弹起(碰撞时间极短,可忽略不计),其速度随时间变化的关系图线如图3所示,在下落过程中方框平面保持水平,不计空气阻力,重力加速度为g。
(1)求在0~15t0时间内,方框中的最大电流Im;
(2)若要提高方框的最大速度,可采取什么措施,写出必要的文字说明和证明过程(设磁场区域足够长,写出一种措施即可);
(3)估算在0~15t0时间内,安培力做的功。



图3 方框速度随时间变化的关系
解答:
(1)
当v=vm=8v0时,I有最大值,![]() ……………………………(6分)
……………………………(6分)
(2)设金属线框的密度为d。当方框速度v=vm时,根据牛顿第二定律有
![]()
因为 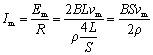
![]()
所以 ![]()
可采取的措施有
a.减小磁场的磁感应强度B;
b.更换材料,使d和ρ的乘积变大 ……………………………………………(6分)
(3)设方框开始下落时距底面的高度为h1,第一次弹起后达到的最大高度为h2。
在下落过程中,根据动能定理有:
![]()
在上升过程中,根据动能定理有:
![]()
又因为 ![]()
由图3可知:![]()
![]() ~
~![]() 均可)
均可)
![]()
![]() ~
~![]() 均可)
均可)
且 ![]()
所以 ![]() (应与h1、h2的值对应) ………(8分)
(应与h1、h2的值对应) ………(8分)


 如图所示,匀强磁场的磁感应强度方向竖直向上,大小为B0用电阻率为ρ、横截面积为S的导线做成的边长为l的正方形线圈abcd水平放置,OO'为过ad、bc两边中点的直线.线圈全部都位于磁场中.现把线圈右半部分固定不动,而把线圈左半部分以OO'为轴向上转动60°,如图中虚线所示.
如图所示,匀强磁场的磁感应强度方向竖直向上,大小为B0用电阻率为ρ、横截面积为S的导线做成的边长为l的正方形线圈abcd水平放置,OO'为过ad、bc两边中点的直线.线圈全部都位于磁场中.现把线圈右半部分固定不动,而把线圈左半部分以OO'为轴向上转动60°,如图中虚线所示.