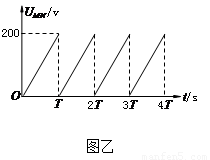题目内容
如图甲所示,带正电的粒子以水平速度v从平行金属板MN间中线OO′连续射入电场中,MN板间接有如图乙所示的随时间t变化的电压UMN,电压变化周期T=0.1s,两板间电场可看做均匀的,且两板外无电场.紧邻金属板右侧有垂直纸面向里的匀强磁场B,分界线为CD,AB为荧光屏.金属板间距为d,长度为l,磁场B的宽度为d.已知:B=5×10-3T,l=d=0.2mv=105m/s,带正电的粒子的比荷为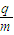 =108C/kg,重力忽略不计.试求:
=108C/kg,重力忽略不计.试求: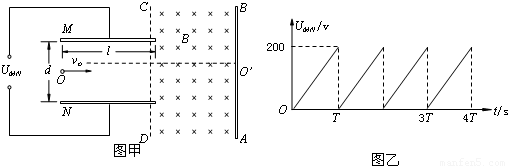
(1)带电粒子进入磁场做圆周运动的最小半径;
(2)带电粒子射出电场时的最大速度;
(3)带电粒子打在荧光屏AB上的范围.
【答案】分析:(1)t=0时刻射入电场的带电粒子不被加速,进入磁场做圆周运动的半径最小,洛伦兹力提供向心力求出带电粒子在磁场中运动的轨道半径;
(2)将带电粒子的运动沿着水平方向和竖直方向正交分解,水平方向为匀速运动,竖直方向为初速度为零的匀加速运动,根据运动学公式列式求解;
带电粒子从平行板边缘射出时,电场力做功最多,获得的动能最大,根据动能定理列式求解;
(3)经过电场偏转后,粒子速度向上偏转或向下偏转,画出可能的轨迹图,根据洛伦兹力提供向心力得到轨道半径,通过几何关系求解.
解答:解:(1)t=0时刻射入电场的带电粒子不被加速,进入磁场做圆周运动的半径最小,
粒子在磁场中运动时有qvB=
rmin=
(2)因带电粒子通过电场时间t= s<T
s<T
所以带电粒子通过电场过程中可认为电场恒定不变.
设两板间电压为U1时,带电粒子能从N板右边缘飞出,


在电压低于或等于100V时,带电粒子才能从两板间射出电场,故U1=100V时,
带电粒子射出电场速度最大,q
解得:
(3)t=0时刻进入电场中粒子,进入磁场中圆轨迹半径最小,打在荧光屏上最高点E,
O′E=rmin=0.2m
从N板右边缘射出粒子,进入磁场中圆轨迹半径最大,

解得:
因 ,故tanθ=
,故tanθ= ,θ=45°,
,θ=45°,

O2P=2× =
= =0.2
=0.2 m=rmax
m=rmax
所以从P点射出粒子轨迹圆心O2正好在
荧光屏上且O2与M板在同一水平线上,0′O2= =0.1m,
=0.1m,
O′F=
带电粒子打在荧光屏AB上范围为:
EF=O′E+O′F=0.38m
答:(1)带电粒子进入磁场做圆周运动的最小半径为0.2m;
(2)带电粒子射出电场时的最大速度为1.41×105m/s;
(3)带电粒子打在荧光屏AB上的范围为0.38m.
点评:本题关键是画出粒子进入磁场后的各种可能的运动轨迹,根据洛伦兹力提供向心力列式后得出半径,然后求出磁偏转的距离表达式,并得出回旋角度的范围,从而得到磁偏转的范围.
(2)将带电粒子的运动沿着水平方向和竖直方向正交分解,水平方向为匀速运动,竖直方向为初速度为零的匀加速运动,根据运动学公式列式求解;
带电粒子从平行板边缘射出时,电场力做功最多,获得的动能最大,根据动能定理列式求解;
(3)经过电场偏转后,粒子速度向上偏转或向下偏转,画出可能的轨迹图,根据洛伦兹力提供向心力得到轨道半径,通过几何关系求解.
解答:解:(1)t=0时刻射入电场的带电粒子不被加速,进入磁场做圆周运动的半径最小,
粒子在磁场中运动时有qvB=

rmin=

(2)因带电粒子通过电场时间t=
 s<T
s<T所以带电粒子通过电场过程中可认为电场恒定不变.
设两板间电压为U1时,带电粒子能从N板右边缘飞出,


在电压低于或等于100V时,带电粒子才能从两板间射出电场,故U1=100V时,
带电粒子射出电场速度最大,q

解得:

(3)t=0时刻进入电场中粒子,进入磁场中圆轨迹半径最小,打在荧光屏上最高点E,
O′E=rmin=0.2m
从N板右边缘射出粒子,进入磁场中圆轨迹半径最大,

解得:

因
 ,故tanθ=
,故tanθ= ,θ=45°,
,θ=45°,
O2P=2×
 =
= =0.2
=0.2 m=rmax
m=rmax所以从P点射出粒子轨迹圆心O2正好在
荧光屏上且O2与M板在同一水平线上,0′O2=
 =0.1m,
=0.1m,O′F=

带电粒子打在荧光屏AB上范围为:
EF=O′E+O′F=0.38m
答:(1)带电粒子进入磁场做圆周运动的最小半径为0.2m;
(2)带电粒子射出电场时的最大速度为1.41×105m/s;
(3)带电粒子打在荧光屏AB上的范围为0.38m.
点评:本题关键是画出粒子进入磁场后的各种可能的运动轨迹,根据洛伦兹力提供向心力列式后得出半径,然后求出磁偏转的距离表达式,并得出回旋角度的范围,从而得到磁偏转的范围.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
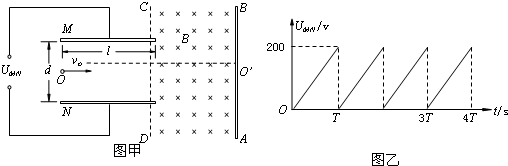
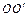 连续射入电场中,MN板间接有如图乙所示的随时间t变化的电压
连续射入电场中,MN板间接有如图乙所示的随时间t变化的电压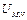 ,电压变化周期T=0.1s,两板间电场可看做均匀的,且两板外无电场. 紧邻金属板右侧有垂直纸面向里的匀强磁场B,分界线为CD,AB为荧光屏. 金属板间距为d,长度为l,磁场B的宽度为d. 已知:
,电压变化周期T=0.1s,两板间电场可看做均匀的,且两板外无电场. 紧邻金属板右侧有垂直纸面向里的匀强磁场B,分界线为CD,AB为荧光屏. 金属板间距为d,长度为l,磁场B的宽度为d. 已知: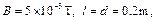
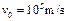 ,带正电的粒子的比荷为q/m=108C/kg,重力忽略不计. 试求:
,带正电的粒子的比荷为q/m=108C/kg,重力忽略不计. 试求: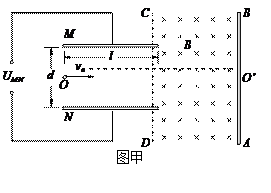
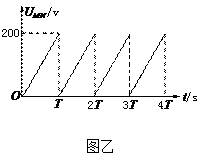
 连续射入电场中,MN板间接有如图乙所示的随时间t变化的电压
连续射入电场中,MN板间接有如图乙所示的随时间t变化的电压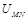 ,电压变化周期T=0.1s,两板间电场可看做均匀的,且两板外无电场. 紧邻金属板右侧有垂直纸面向里的匀强磁场B,分界线为CD,AB为荧光屏. 金属板间距为d,长度为l,磁场B的宽度为d. 已知:
,电压变化周期T=0.1s,两板间电场可看做均匀的,且两板外无电场. 紧邻金属板右侧有垂直纸面向里的匀强磁场B,分界线为CD,AB为荧光屏. 金属板间距为d,长度为l,磁场B的宽度为d. 已知: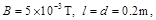
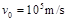 ,带正电的粒子的比荷为q/m=108C/kg,重力忽略不计. 试求:
,带正电的粒子的比荷为q/m=108C/kg,重力忽略不计. 试求: