题目内容
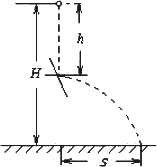
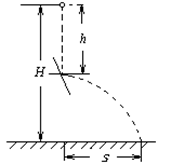
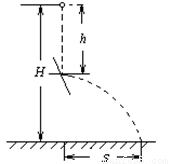
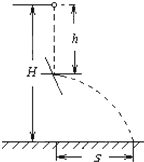 如图所示,一小球由距地面高为H处自由下落,当它下落了距离为h时与斜面相碰,碰后小球以原来的速率水平抛出.当h=
如图所示,一小球由距地面高为H处自由下落,当它下落了距离为h时与斜面相碰,碰后小球以原来的速率水平抛出.当h=分析:根据自由落体运动的高度求出与斜面相碰的速度,从而得知平抛运动的初速度,结合平抛运动在水平方向和竖直方向上的运动规律求出水平位移的表达式,通过二次函数求极值求出何时水平位移有最大值.
解答:解:小球自由下落h时的速度v=
.
根据H-h=
gt2得,t=
.
则水平位移x=vt=
?
=
=
可知当h=
时,水平位移有最大值.
故答案为:
.
| 2gh |
根据H-h=
| 1 |
| 2 |
|
则水平位移x=vt=
| 2gh |
|
| 4h(H-h) |
| -(2h-H)2+H2 |
可知当h=
| H |
| 2 |
故答案为:
| 1 |
| 2 |
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式进行求解.本题对数学能力的要求较高.

练习册系列答案
相关题目