题目内容
角速度计可测量航天器自转的角速度ω,其结构如图所示.当系统绕OO′转动时,元件A在光滑杆上发生滑动,并输出电压信号成为航天器的制导信号源.已知A质量为m,弹簧的劲度系数为k,原长为L0,电源电动势为E,内阻不计.滑动变阻器总长为L,电阻分布均匀,系统静止时滑动变阻器滑动头P在中点,与固定接点Q正对,当系统以角速度ω转动时,求:
(1)弹簧形变量x与ω的关系式;
(2)电压表的示数U与角速度ω的函数关系.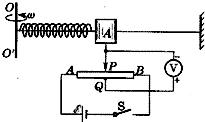
(1)弹簧形变量x与ω的关系式;
(2)电压表的示数U与角速度ω的函数关系.

(1)设系统在水平面内以角速度ω转动时,弹簧伸长的长度为x,则
对元件A,根据牛顿第二定律得
Fn=ma=mω2R,
Fn=kx=mω2(L0+x),
即x=
(2)根据题意可知:电压表的示数U=
=
所以电压表的示数U与角速度ω的函数关系为U=
.
答:(1)弹簧形变量x与ω的关系式为x=
;
(2)电压表的示数U与角速度ω的函数关系为U=
.
对元件A,根据牛顿第二定律得
Fn=ma=mω2R,
Fn=kx=mω2(L0+x),
即x=
| mω2L0 |
| k-mω2 |
(2)根据题意可知:电压表的示数U=
| xE |
| L |
| mω2L0E |
| L(k-mω2) |
所以电压表的示数U与角速度ω的函数关系为U=
| mω2L0E |
| L(k-mω2) |
答:(1)弹簧形变量x与ω的关系式为x=
| mω2L0 |
| k-mω2 |
(2)电压表的示数U与角速度ω的函数关系为U=
| mω2L0E |
| L(k-mω2) |

练习册系列答案
相关题目
 角速度计可测量航天器自转的角速度ω,其结构如图所示.当系统绕OO′转动时,元件A在光滑杆上发生滑动,并输出电压信号成为航天器的制导信号源.已知A质量为m,弹簧的劲度系数为k,原长为L0,电源电动势为E,内阻不计.滑动变阻器总长为L,电阻分布均匀,系统静止时滑动变阻器滑动头P在中点,与固定接点Q正对,当系统以角速度ω转动时,求:
角速度计可测量航天器自转的角速度ω,其结构如图所示.当系统绕OO′转动时,元件A在光滑杆上发生滑动,并输出电压信号成为航天器的制导信号源.已知A质量为m,弹簧的劲度系数为k,原长为L0,电源电动势为E,内阻不计.滑动变阻器总长为L,电阻分布均匀,系统静止时滑动变阻器滑动头P在中点,与固定接点Q正对,当系统以角速度ω转动时,求: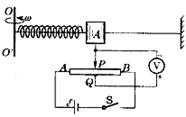 角速度计可测量航天器自转的角速度ω,其结构如图所示.当系统绕OO′轴转动时,元件A在光滑杆上发生滑动,并输出电压信号成为航天器的制导信号源.已知A质量为m,弹簧的劲度系数为k,原长为L0,电源电动势为E,内阻不计.滑动变阻器总长为L,电阻分布均匀,系统静止时滑动变阻器滑动头P在中点,与固定接点Q正对,当系统以角速度ω转动时,求:
角速度计可测量航天器自转的角速度ω,其结构如图所示.当系统绕OO′轴转动时,元件A在光滑杆上发生滑动,并输出电压信号成为航天器的制导信号源.已知A质量为m,弹簧的劲度系数为k,原长为L0,电源电动势为E,内阻不计.滑动变阻器总长为L,电阻分布均匀,系统静止时滑动变阻器滑动头P在中点,与固定接点Q正对,当系统以角速度ω转动时,求: 角速度计可测量航天器自转的角速度ω,其结构如图所示.当系统绕OO′转动时,元件A在光滑杆上发生滑动,并输出电压信号成为航天器的制导信号源.已知A质量为m,弹簧的劲度系数为k,原长为L0,电源电动势为E,内阻不计.滑动变阻器总长为L,电阻分布均匀,系统静止时滑动变阻器滑动头P在中点,与固定接点Q正对,当系统以角速度ω转动时,求:
角速度计可测量航天器自转的角速度ω,其结构如图所示.当系统绕OO′转动时,元件A在光滑杆上发生滑动,并输出电压信号成为航天器的制导信号源.已知A质量为m,弹簧的劲度系数为k,原长为L0,电源电动势为E,内阻不计.滑动变阻器总长为L,电阻分布均匀,系统静止时滑动变阻器滑动头P在中点,与固定接点Q正对,当系统以角速度ω转动时,求: