题目内容
如图所示，平行金属导轨宽度为l=0.6m，与水平面间的倾角为θ=37o，导轨电阻不计，底端接有阻值为R=3Ω的定值电阻，磁感强度为B=1T的匀强磁场垂直穿过导轨平面。有一质量为m=0.2kg，长也为l的导体棒受导轨上两支柱p支撑静止在ab位置，导体棒的电阻为Ro=1Ω，它与导轨之间的动摩擦因数为μ=0.3。导体棒获得平行斜面的初速vo=10m/s向上滑行最远至a/b/位置，所滑行距离为s=4m。(sin37o=0.6，cos37o=0.8，重力加速度g=10m/s2)。问：
（1）把运动导体棒视为电源，最大输出功率是多少？
（2）上滑过程中导体棒所受的安培力做了多少功？
（3）以ab位置为零势点，若导体棒从ab上滑d=3m过程中电阻R发出的热量QR=2.1J，此时导体棒的机械能E /为多大？
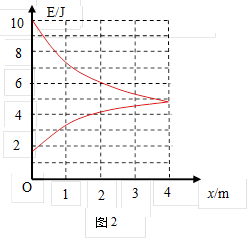
（4）在图2中画出图线，要求能反映导体棒在上滑和下滑过程中机械能E随位移x变化的大致规律。（x正方向沿斜面向上，坐标原点O在ab位置）
（1）6.75W（2）J（3）
（4）见解析
解析:先根据最大速度时，电流最大，从而求出最大功率；根据动能定理求出安培力所做的功；根据电阻R上产生的焦耳热求出总的热量，利用功能关系求解机械能；写出机械能的表达式，根据表达式画出图象。
(1) （4分）由闭合电路欧姆定律
（2分）
最大输出功率为 （2分）
(2) （3分）安培力做负功，由动能定理
-（2分）
代入数据得J （1分）
(3) （4分），由串联电路功率关系得焦耳热
J （2分）
根据功能原理：，
代入数据解得J（2分）
(4) （3分） 棒至a/b/位置时机械能为J，由能量关系分析，棒回到ab位置时速度不可能为零，这时的机械能
0＜E末＜（4.8-1.92=2.88）J
画出的大致图线如右图所示，图线变化趋势与截距正确给3分，有错相应扣分。
第1卷单元月考期中期末系列答案
如图所示，倾角为θ=30°，宽度为L=1m的足够长的U型平行光滑金属导轨固定在磁感应强度B=1T且范围充分大的匀强磁场中，磁场方向垂直导轨平面斜向上，现用平行于导轨、功率恒为6W的牵引力F，牵引一根质量m=0.2kg、电阻R=1Ω的导棒ab由静止沿导轨向上移动（ab棒始终与导轨接触良好且垂直）．当金属导棒ab移动s=2.8m时，获得稳定速度．在此过程中金属导棒产生的热量为Q=5.8J（不计导轨电阻及一切摩擦，g取10m/s2）．
如图所示，在匀强磁场中放有平行铜导轨，它与大导线圈M相连接，要使小导线圈N获得顺时针方向的感应电流，则放在导轨中的裸金属棒ab的运动情况是（两导线圈共面位置）（ ）
（2010?南通模拟）如图所示，左右两边分别有两根平行金属导轨相距为L，左导轨与水平面夹30°角，右导轨与水平面夹60°角，左右导轨上端用导线连接．导轨空间内存在匀强磁场，左边的导轨处在方向沿左导轨平面斜向下，磁感应强度大小为B的磁场中．右边的导轨处在垂直于右导轨斜向上，磁感应强度大小也为B的磁场中．质量均为m的导杆ab和cd垂直导轨分别放于左右两侧导轨上，已知两导杆与两侧导轨间动摩擦因数均为μ=
