题目内容
我国2007年10月24日发射的“嫦娥一号”月球卫星经过四次变轨后其绕地球运行的椭圆轨道的远地点D靠近了距地面38万公里的月球轨道.我国未来将建立月球基地,并在绕月轨道上建造空间站,如图所示.要和空间站对接的航天飞机关闭动力,在月球引力作用下经椭圆轨道向月球靠近,并将与空间站在E处对接.已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )
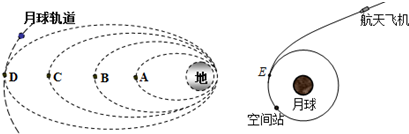

| A、图中航天飞机在飞向E处的过程中,月球引力做正功,所以在E处由椭圆轨道可直接进入空间站圆周轨道,不需要变速 | B、如果忽略月球引力的影响,“嫦娥一号”通过远地点A,B,C,D时,在D点线速度最大,加速度最小 | C、根据题中条件可以算出月球质量 | D、如果忽略月球引力的影响,“嫦娥一号”通过远地点A,B,C,D时,和地球系统所决定的机械能,A点最大,D点最小 |
分析:航天飞机在飞向E处的过程中,飞船与月球的引力的方向和飞船的运动方向之间的夹角小于90°,所以月球引力做正功;椭圆轨道和圆轨道是不同的轨道;航天经过E处时的加速度与空间站经过E处时的加速度都是万有引力产生的.
解答:解:A、航天飞机在飞向E处的过程中,飞船与月球的引力的方向和飞船的运动方向之间的夹角小于90°,所以月球引力做正功;椭圆轨道和圆轨道是不同的轨道,航天飞机不可能自主改变轨道,只有在减速后,才能进入空间站轨道;故A错误;
B、根据圆轨道公式v=
,圆轨道上半径越大,线速度越小;而卫星在椭圆轨道上同一点的线速度比对应圆轨道的线速度小,故在D点线速度最小;根据万有引力定律,在D点万有引力最小,根据牛顿第二定律,加速度也是最小;故B错误;
C、已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,根据万有引力提供向心力,有:
G
=m(
)2r
解得:M=
故C正确;
D、卫星在同一轨道运动时机械能守恒,经过近地点时,D点所在轨道对应的速度最大,故机械能最大,即D点的机械能最大,故D错误;
故选:C.
B、根据圆轨道公式v=
|
C、已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,根据万有引力提供向心力,有:
G
| Mm |
| r2 |
| 2π |
| T |
解得:M=
| GT2 |
| 4π2r3 |
故C正确;
D、卫星在同一轨道运动时机械能守恒,经过近地点时,D点所在轨道对应的速度最大,故机械能最大,即D点的机械能最大,故D错误;
故选:C.
点评:本题是变轨问题,在圆轨道运行时万有引力提供向心力,根据牛顿第二定律列式求解;椭圆轨道还是与正圆轨道相比较.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 我国2007年10月24日发射的“嫦娥一号”月球卫星经过四次变轨后其绕地球运行的椭圆轨道的远地点D靠近了距地面38万公里的月球轨道.如果忽略月球引力的影响,有关“嫦娥一号”通过远地点A,B,C,D的物理量说法正确的是( )
我国2007年10月24日发射的“嫦娥一号”月球卫星经过四次变轨后其绕地球运行的椭圆轨道的远地点D靠近了距地面38万公里的月球轨道.如果忽略月球引力的影响,有关“嫦娥一号”通过远地点A,B,C,D的物理量说法正确的是( )