题目内容
一汽车以72km/h的速度在一平直公路上匀速行驶,突然发现前方4m处有一轿车也在同向匀速前进,于是汽车司机马上刹车,设汽车司机的反应时间为0.3s,汽车与地面间的动摩擦因数为0.5,要使两车不相撞,则要求前方轿车行驶的最小速度为多大?(g取10m/s2)
【答案】分析:汽车在反应时间内做匀速直线运动,刹车后做匀减速直线运动,临界情况是速度相同时,恰好不相撞,结合速度时间公式和位移时间公式求出前方轿车行驶的最小速度.
解答:解:72km/h=20m/s,a=μg=5m/s2.
设速度相同时刚好撞上,则:
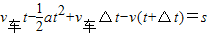
v车-at=v
代入数据有:
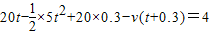
20-5t=v
解得t=1s.
故要求前方汽车的最小速度为:v=20-5t=15m/s.
答:前方轿车行驶的最小速度为15m/s.
点评:解决本题的关键抓住临界情况,速度相同时恰好不相撞,结合运动学公式进行求解.
解答:解:72km/h=20m/s,a=μg=5m/s2.
设速度相同时刚好撞上,则:
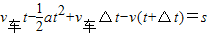
v车-at=v
代入数据有:
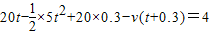
20-5t=v
解得t=1s.
故要求前方汽车的最小速度为:v=20-5t=15m/s.
答:前方轿车行驶的最小速度为15m/s.
点评:解决本题的关键抓住临界情况,速度相同时恰好不相撞,结合运动学公式进行求解.

练习册系列答案
相关题目