题目内容
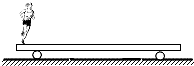 如图所示,长12m,质量100kg的小车静止在光滑水平地面上.一质量为50kg的人从小车左端,以4m/s2加速度向右匀加速跑至小车的右端(人的初速度为零).求:
如图所示,长12m,质量100kg的小车静止在光滑水平地面上.一质量为50kg的人从小车左端,以4m/s2加速度向右匀加速跑至小车的右端(人的初速度为零).求:(1)小车的加速度大小;
(2)人从开始起跑至到达小车右端所经历的时间;
(3)人从开始起跑至到达小车右端对小车所做的功.
分析:(1)对人由牛顿第二定律即可求得所受摩擦力;由牛顿第三定律可知人对小车的摩擦力大小等于人所受摩擦力大小,对小车运用牛顿第二定律即可求出加速度;
(2)设人从左端跑到右端时间为t,由运动学公式求出各自的位移表达式,根据位移之和等于L即可求解.
(3)根据动能定理即可求得人从开始起跑至到达小车右端对小车所做的功.
(2)设人从左端跑到右端时间为t,由运动学公式求出各自的位移表达式,根据位移之和等于L即可求解.
(3)根据动能定理即可求得人从开始起跑至到达小车右端对小车所做的功.
解答:解:(1)设人的质量为m,加速度为a1,人受的摩擦力为f,由牛顿第二定律有:
f=ma1=200N
由牛顿第三定律可知人对小车的摩擦力大小f′=200N
设小车的质量为M,加速度为a2,对小车由牛顿第二定律有:
f′=Ma2
代入数据得a2=2m/s2
(2)设人从左端跑到右端时间为t,由运动学公式:
L=
a1t2+
a2t2
解得t=2s
(3)木板末速度v2=a2t
根据动能定理得:
W=
Mv22=800J
答:(1)小车的加速度大小为2m/s2;
(2)人从开始起跑至到达小车右端所经历的时间为2s;
(3)人从开始起跑至到达小车右端对小车所做的功为800J.
f=ma1=200N
由牛顿第三定律可知人对小车的摩擦力大小f′=200N
设小车的质量为M,加速度为a2,对小车由牛顿第二定律有:
f′=Ma2
代入数据得a2=2m/s2
(2)设人从左端跑到右端时间为t,由运动学公式:
L=
| 1 |
| 2 |
| 1 |
| 2 |
解得t=2s
(3)木板末速度v2=a2t
根据动能定理得:
W=
| 1 |
| 2 |
答:(1)小车的加速度大小为2m/s2;
(2)人从开始起跑至到达小车右端所经历的时间为2s;
(3)人从开始起跑至到达小车右端对小车所做的功为800J.
点评:本题主要考查了牛顿第二定律的直接应用,要抓住人与木板的位移关系求解,难度适中.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图所示,长12m的木板右端固定一立柱,板和立柱的总质量为50kg,木板置于水平地面上,木板与地面间的动摩擦因数为0.1,质量为50kg的人立于木板左端,木板与人均静止,若人以4m/s2的加速度匀加速度向右奔跑至板的右端并立即抱住立柱,求:
如图所示,长12m的木板右端固定一立柱,板和立柱的总质量为50kg,木板置于水平地面上,木板与地面间的动摩擦因数为0.1,质量为50kg的人立于木板左端,木板与人均静止,若人以4m/s2的加速度匀加速度向右奔跑至板的右端并立即抱住立柱,求: 如图所示,长12m质量为50kg的木版右端有一立柱.木板置于水平地面上,木板与地面间的动摩擦因数为0.1,质量为50kg的人立于木板左端,木板与人均静止,当人以4m/s2的加速度匀加速向右奔跑至板的右端时,立刻抱住木柱,试求:
如图所示,长12m质量为50kg的木版右端有一立柱.木板置于水平地面上,木板与地面间的动摩擦因数为0.1,质量为50kg的人立于木板左端,木板与人均静止,当人以4m/s2的加速度匀加速向右奔跑至板的右端时,立刻抱住木柱,试求: 如图所示,长12m质量为50kg的木板右端有一立柱.木板置于水平地面上,木板与地面间的动摩擦因数为0.1,质量为50kg的人立于木板左端,木板与人均静止,当人以4m/s2的加速度匀加速向右奔跑至板的右端时,立刻抱住立柱,取(g=10m/s)试求:
如图所示,长12m质量为50kg的木板右端有一立柱.木板置于水平地面上,木板与地面间的动摩擦因数为0.1,质量为50kg的人立于木板左端,木板与人均静止,当人以4m/s2的加速度匀加速向右奔跑至板的右端时,立刻抱住立柱,取(g=10m/s)试求: 如图所示,长12m的木板质量为50kg,木板置于水平地面上,木板与地面间的动摩擦因数为0.1,质量为50kg的人立于木板左端,木板与人均静止,人以4m/s2的加速度匀加速向右奔跑至板的右端,求:
如图所示,长12m的木板质量为50kg,木板置于水平地面上,木板与地面间的动摩擦因数为0.1,质量为50kg的人立于木板左端,木板与人均静止,人以4m/s2的加速度匀加速向右奔跑至板的右端,求: