题目内容
一个具有13.6eV动能的基态原子与一个静止的基态原子发生对心正碰,试证明:两氢原子之间的碰撞动能守恒.
解析:
|
方法一 设氢原子的质量为m,运动的氢原子的初速度为v,碰后速度为 式中 联立以上各式并化简可得: 由玻尔理论可知,基态的氢原子被激发到激发态时所需的最小能量为
比较⑤⑥式可知,无法互相满足,即该碰撞没有动能损失. 方法二 假设两个氢原子碰撞后的速度相同并设为 由动量守恒可知:mv= 解之,得: 此过程中损失的动能: 上式表明, 处于静止的基态氢原子具有的能量 思路一 利用判别式法.两个氢原子的碰撞过程符合动量守恒条件,且符合能量守恒,若碰撞过程中有动能损失,则应能得到碰后氢原子运动速度与损失的动能 思路二 利用假设法.两个氢原子发生对心正碰,若碰后的速度相同,则机械能损失最大.假设两个原子碰撞后的速度相同,则可求出损失的动能.再比较氢原子跃迁时需要吸收的能量,则可进行判断这两个氢原子的碰撞是否有动能损失. |
提示:
|
力学中常用到的“弹性碰撞”只有在微观领域中才能发生,本题就是一个很好的证明.读者可自行分析欲使这两个氢原子在碰撞过程中有动能损失,即电子跃迁到激发态,运动的原子的初动能应满足何种条件? 本题是一道力学与原子物理学的综合题目,要求学生具有较强的综合能力,此题的关键是明确损失的动能必将转化为氢原子的能量,而使氢原子发生跃迁.同时应注意:原子跃迁所需的能量是不连续的. |

氦原子被电离一个核外电子,形成类氢结构的氦离子。已知基态的氦离子能量为E1=-
54.4eV,氦离子能级的示意图如图所示。在具有下列能量的光子中,不能被基态氦离子吸收
而发生跃迁的是 ( )
|
E5 |
0 |
|
E4 |
3.4eV |
|
E3 |
6.0eV |
|
E2 |
13.6eV |
|
E1 |
54.4eV |
A.40.8eV
B.43.2ev
C.51.0eV
D.54.4eV
54.4eV,氦离子能级的示意图如图所示。在具有下列能量的光子中,不能被基态氦离子吸收
而发生跃迁的是 ( )
|
E5 |
0 |
|
E4 |
3.4eV |
|
E3 |
6.0eV |
|
E2 |
13.6eV |
|
E1 |
54.4eV |
A.40.8eV
B.43.2ev
C.51.0eV
D.54.4eV
 ,静止的氢原子碰后速度为
,静止的氢原子碰后速度为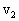 .
.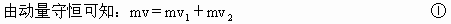

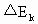 为两氢原子在碰撞过程中损失的动能.
为两氢原子在碰撞过程中损失的动能.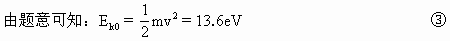
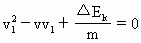


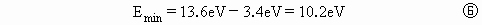
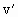 .
.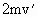
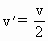
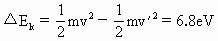
 不足以使氢原子发生跃迁,即碰撞过程中两个氢原子都没有吸收能量,碰撞过程中无动能损失.
不足以使氢原子发生跃迁,即碰撞过程中两个氢原子都没有吸收能量,碰撞过程中无动能损失.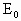 =13.6eV,依据玻尔的氢原子理论,电子跃迁时将吸收或放出能量,吸收或放出的能量等于两个能量状态的差值.对于本题而言,若两个氢原子发生碰撞损失动能,则依据能量守恒定律,损失的动能必将转化成电子的能量使电子发生跃迁.
=13.6eV,依据玻尔的氢原子理论,电子跃迁时将吸收或放出能量,吸收或放出的能量等于两个能量状态的差值.对于本题而言,若两个氢原子发生碰撞损失动能,则依据能量守恒定律,损失的动能必将转化成电子的能量使电子发生跃迁.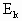 之间的关系,且碰后氢原子的速度应有实数解,并且损失的动能应该满足电子跃迁时需要吸收的能量.
之间的关系,且碰后氢原子的速度应有实数解,并且损失的动能应该满足电子跃迁时需要吸收的能量.