题目内容
磁悬浮列车以大小为v的速度沿赤道高速向东行驶,某时刻人造地球卫星A正好经过磁悬浮列车正上方,运动方向与磁悬浮列车的运动方向相同,列车行驶路程s后,卫星又一次通过列车的正上方.已知地球的半径为R,自转周期为T0,地球表面的重力加速度为g,求卫星离地面的高度.
分析:某时刻人造地球卫星A正好经过磁悬浮列车正上方,卫星又一次通过列车的正上方.根据圆周运动的几何关系找出卫星转过的角度的关系表达式.
根据万有引力提供向心力
根据万有引力提供向心力
解答:解:设卫星的角速度为ω,
在列车行驶路程s的时间t=
内,卫星又一次通过列车的正上方.
所以卫星转过的角度是ωt=
+
+2π
根据万有引力提供向心力得
=mω2(R+h)
根据黄金代换GM=gR2
解得:h=
-R.
答:卫星离地面的高度是
-R.
在列车行驶路程s的时间t=
| s |
| v |
所以卫星转过的角度是ωt=
| 2πt |
| T0 |
| vt |
| R |
根据万有引力提供向心力得
| GMm |
| (R+h)2 |
根据黄金代换GM=gR2
解得:h=
| 3 |
| ||||||||
答:卫星离地面的高度是
| 3 |
| ||||||||
点评:本题关键:(1)根据万有引力提供向心力表示轨道半径;(2)根据地球表面重力等于万有引力得到黄金代换式;(3)根据转动的角度列式.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
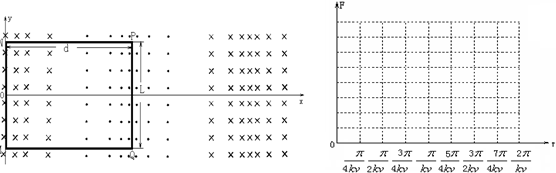
 (2008?天津)磁悬浮列车是一种高速低耗的新型交通工具.它的驱动系统简化为如下模型,固定在列车下端的动力绕组可视为一个矩形纯电阻金属框,电阻为R,金属框置于xOy平面内,长边MN长为l平行于y轴,宽度为d的NP边平行于x轴,如图1所示.列车轨道沿Ox方向,轨道区域内存在垂直于金属框平面的磁场,磁感应强度B沿Ox方向按正弦规律分布,其空间周期为λ,最大值为B0,如图2所示,金属框同一长边上各处的磁感应强度相同,整个磁场以速度v0沿Ox方向匀速平移.设在短暂时间内,MM、PQ边所在位置的磁感应强度随时间的变化可以忽略,并忽略一切阻力.列车在驱动系统作用下沿Ox方向加速行驶,某时刻速度为v(v<v0).
(2008?天津)磁悬浮列车是一种高速低耗的新型交通工具.它的驱动系统简化为如下模型,固定在列车下端的动力绕组可视为一个矩形纯电阻金属框,电阻为R,金属框置于xOy平面内,长边MN长为l平行于y轴,宽度为d的NP边平行于x轴,如图1所示.列车轨道沿Ox方向,轨道区域内存在垂直于金属框平面的磁场,磁感应强度B沿Ox方向按正弦规律分布,其空间周期为λ,最大值为B0,如图2所示,金属框同一长边上各处的磁感应强度相同,整个磁场以速度v0沿Ox方向匀速平移.设在短暂时间内,MM、PQ边所在位置的磁感应强度随时间的变化可以忽略,并忽略一切阻力.列车在驱动系统作用下沿Ox方向加速行驶,某时刻速度为v(v<v0).