题目内容
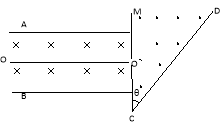
【题目】如图所示,两平行金属板AB中间有互相垂直的匀强电场和匀强磁场。A板带正电荷,B板带等量负电荷,板间电场强度为E;磁场方向垂直纸面向里,磁感应强度为B1。平行金属板右侧有一挡板M,中间有小孔O′,OO′是平行于两金属板的中心线。挡板右侧有垂直纸面向外的匀强磁场,磁场应强度为B2。CD为磁场B2边界上的一绝缘板,它与M板的夹角θ=45°,O′C=a,现有大量质量均为m,含有不同电荷量、不同速度的正负带电粒子(不计重力),自O点沿OO′方向进入电磁场区域,其中有些粒子沿直线OO′方向运动,并进入匀强磁场B2中,求:
(1)进入匀强磁场B2的带电粒子的速度;
(2)能击中绝缘板CD的粒子中,所带电荷量的最大值;
(3)绝缘板CD上被带电粒子击中区域的长度;
【答案】(1)![]() (2)(
(2)(![]() +1)
+1)![]() (3)2a
(3)2a
【解析】
试题分析:(1)沿直线OO′运动的带电粒子,设进入匀强磁场B2的带电粒子的速度为v,
根据B1qv=qE
解得:![]()
(2)粒子进入匀强磁场B2中做匀速圆周运动,根据![]() ,
,
解得:![]()
因此,电荷量最大的带电粒子运动的轨道半径最小,设最小半径为r1,此带电粒子运动轨迹与CD板相切,
则有:r1+![]() r1=a,
r1=a,
解得:r1=(![]() -1)a.
-1)a.
电荷量最大值q=(![]() +1)
+1)![]() .
.
(3)带负电的粒子在磁场B2中向上偏转,某带负电粒子轨迹与CD相切,设半径为r2,
依题意r2+a=![]() r2
r2
解得:r2=(![]() +1)a
+1)a
则CD板上被带电粒子击中区域的长度为X=r2-r1=2a

练习册系列答案
相关题目