��Ŀ����
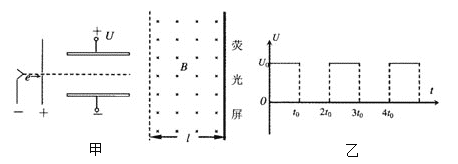
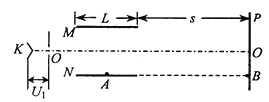
����Ŀ����ͼ��ʾ�����������ֱ��������ǿ�糡E1��E2����֪��������L��0.8m���������㹻���� ![]() ����ˮƽ��45���б�����Ϸ���E2��2kV/m����ˮƽ����Ե����B��L��2.8m����mB��1.6kg���ڹ⻬ˮƽ���ϣ������������������߽�ƽ�롣������Ϊq����1.6��10��3C����mA��1.6kg�Ĵ�����A����Ϊ�ʵ㣬��ľ���Ķ�Ħ����������0.1������ľ���������ɾ�ֹ�ͷš�(g��10m/s2)��
����ˮƽ��45���б�����Ϸ���E2��2kV/m����ˮƽ����Ե����B��L��2.8m����mB��1.6kg���ڹ⻬ˮƽ���ϣ������������������߽�ƽ�롣������Ϊq����1.6��10��3C����mA��1.6kg�Ĵ�����A����Ϊ�ʵ㣬��ľ���Ķ�Ħ����������0.1������ľ���������ɾ�ֹ�ͷš�(g��10m/s2)��

(1)������A����������ʱ���ٶ�
(2)ľ��B�������ٶ�
(3)������������Ħ������������
���𰸡���1��4m/s����2��![]() ��3��
��3��![]()
����������1���������ڵ�һ�������˶�ʱ��������������֪�� ![]()
����ľ��֮��û��Ħ�����������嵥�������ڵ�һ�������˶�����ˮƽ�����ϣ� ��ţ�ٵڶ����ɵã� ![]() ���������ݽ�ã�
���������ݽ�ã�
![]() ��
��
���ȱ����˶����ٶ�λ�ƹ�ʽ�ã� ![]() ���������ݽ�ã�
���������ݽ�ã� ![]() ��
��
��2�������������ڶ�����ʱ���ֱ��A��B��ABϵͳ��ţ�ٵڶ�����������ٶȣ�Ȼ��Ӧ���˶�ѧ��ʽ���B���ٶ�����ţ�ٵڶ����ɵã�
��A�� ![]() ���������ݽ�ã�
���������ݽ�ã� ![]() ��
��
��B�� ![]() ����
���� ![]() ��
��
�辭ʱ��t��A��B�ٶ���ȣ���Ϊ![]() ���ٶ���Ⱥ���ٶ�Ϊ
���ٶ���Ⱥ���ٶ�Ϊ![]() ��
��
���ȱ����˶����ٶ�λ�ƹ�ʽ��![]() ���������ݽ��t=1s��
���������ݽ��t=1s��
��λ�ƹ�ʽ�ã� ![]()
![]() ��
��
�������ݽ�ã� ![]() ��
�� ![]() ����
���� ![]() ��
��
��![]() ��
�� ![]() ���ʵ�A���ﱡ���Ҷ�ʱ�����ٶ���ȣ�
���ʵ�A���ﱡ���Ҷ�ʱ�����ٶ���ȣ�
��ţ�ٵڶ����ɵ�![]() ���������ݽ��
���������ݽ��![]() ��
��
���ٶ�λ�ƹ�ʽ�ã� ![]() �����ٶȹ�ʽ�ã�
�����ٶȹ�ʽ�ã� ![]() �����
�����![]() ��
��
�ɹ�ʽ![]()
��һ����A�������ұ��ٵ�4m/s�����У�f=0�� ![]()
�ڶ���A���Ҽ��٣�B���Ҽ��ٹ����У� ![]()
������ABһ�����м��ٵ�0��������ٹ����У�û�����λ�ƣ� ![]()
������������1��4m/s����2��![]() ����3��
����3��![]()

 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�����Ŀ��һ��������ԭ��O�ɾ�ֹ������x����ֱ���˶���Ϊ�о������˶��Ĺ��ɶ���¼�����ڲ�ͬʱ�̵�λ�ú��ٶȣ�������ʾ������
ʱ��t/s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�����x/m | 0 | 0.5 | 2 | 4.5 | 8 | 12 | 16 | 20 |
˲ʱ�ٶ�v/��ms��1�� | 0 | 1 | 2 | 3 | 4 | 4 | 4 | 4 |
��1��������2sĩ���ٶȺ�5.5sĩ���ٶȣ�
��2����2s�ڵ�ƽ���ٶȺ�ǰ5s�ڵ�ƽ���ٶȣ�
��3��ǰ4s�ڵļ��ٶȣ�