题目内容
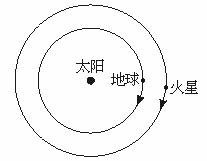
火星和地球绕太阳的运动可以近似地看作在同一平面内同方向的匀速圆周运动,已知火星的轨道半径R1=2.3×1011m,试估算火星冲日的时间间隔(即火星距地球最近时的时间间隔).
答案:
解析:
解析:
解析:火星距地球最近时,太阳、火星、地球三者在一条直线上且火星、地球位于太阳的同侧(如图所示),到下次火星冲日时,应为地球比火星多绕一圈,即多转角度2π所用的时间,已知地球的公转周期T2=1年,由火星与地球的轨道半径可得到火星的公转周期T1,再由圆周运动的角速度与周期的关系即可求解.设火星冲日的时间间隔为ΔT,
则ΔT= 由万有引力充当向心力可得
由②③可得
即T1=T2 将T1=1.9年,T2=1年 代入①式可得ΔT=2.1年. 即火星冲日的时间间隔为2.1年. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 . ①
. ①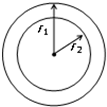 (2010?湖南模拟)如图,火星和地球绕太阳的运动可以近似看作为在同一平面内的同方向的匀速圆周运动,已知火星轨道半径r1=2.3×1011m,地球轨道半径为r2=1.5×1011m,根据你所掌握的物理和天文知识,估算火星与地球相邻两次相距最近的最短时间间隔约为( )
(2010?湖南模拟)如图,火星和地球绕太阳的运动可以近似看作为在同一平面内的同方向的匀速圆周运动,已知火星轨道半径r1=2.3×1011m,地球轨道半径为r2=1.5×1011m,根据你所掌握的物理和天文知识,估算火星与地球相邻两次相距最近的最短时间间隔约为( )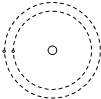 (2004?广州二模)火星和地球绕太阳的运动可以看作为同一平面内同方向的匀速圆周运动,已知火星的轨道半径R=1.5×1011m,地球的轨道半径r=1.0×1011m,从如图所示的火星与地球相距最近的时刻开始计时,估算火星再次与地球相距最近需多少地球年?(保留两位有效数字)
(2004?广州二模)火星和地球绕太阳的运动可以看作为同一平面内同方向的匀速圆周运动,已知火星的轨道半径R=1.5×1011m,地球的轨道半径r=1.0×1011m,从如图所示的火星与地球相距最近的时刻开始计时,估算火星再次与地球相距最近需多少地球年?(保留两位有效数字)