题目内容
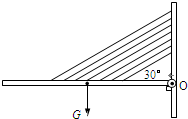（2011?闵行区二模）如图所示是一个单边斜拉桥模型，均匀桥板重为G，可绕通过O点的水平固定轴转动．7根与桥面均成30°角的平行钢索拉住桥面，其中正中间的一根钢索系于桥的重心位置，其余成等距离分布在它的两侧．若每根钢索所受拉力大小相等，则该拉力大小为（ ）分析：以O为支点，分析除O点桥板的受力情况，确定出力臂，根据力矩平衡条件求解拉力大小．可抓住对称性，采用等效的方法：除正中间外的钢索外，其余六根钢索拉力的力矩之和等于正中间钢索的力矩的6倍．
解答：解：设钢板的重心与O的距离为L．
以O为支点，除O点外桥板受到重力G和七根钢索的拉力．由于每根钢索所受拉力大小相等，等距离分布，根据对称性可知，除正中间外的钢索外，其余六根钢索拉力的力矩之和等于正中间钢索的力矩的6倍．则由力矩条件得：
GL=7FLsin30°，得F=
G
故选B
以O为支点，除O点外桥板受到重力G和七根钢索的拉力．由于每根钢索所受拉力大小相等，等距离分布，根据对称性可知，除正中间外的钢索外，其余六根钢索拉力的力矩之和等于正中间钢索的力矩的6倍．则由力矩条件得：
GL=7FLsin30°，得F=
| 2 |
| 7 |
故选B
点评：本题关键要分析钢索分布特点，运用等效的方法分析两侧六根钢索力矩与正中间钢索力矩的关系，即可求解．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
（2011?闵行区二模）如图所示，一根上细下粗、粗端与细端都粗细均匀的玻璃管上端开口、下端封闭，上端足够长，下端（粗端）中间有一段水银封闭了一定质量的理想气体．现对气体缓慢加热，气体温度不断升高，水银柱上升，则被封闭气体体积和热力学温度的关系最接近哪个图象（ ）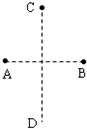
（2011?闵行区二模）如图所示，两个等量同种点电荷分别固定于光滑绝缘水平面上A、B两点．一个带电粒子由C点静止释放，仅受电场力作用，沿着AB中垂线从C点运动到D点（C、D是关于AB对称的两点）．下列关于粒子运动的v-t图象中可能正确的是（ ）
（2011?闵行区二模）如图，箱子A连同固定在箱子底部的竖直杆的总质量为M=10kg．箱子内部高度H=3.75m，杆长h=2.5m，另有一质量为m=2kg的小铁环B套在杆上，从杆的底部以v0=10m/s的初速度开始向上运动，铁环B刚好能到达箱顶，不计空气阻力，g取10m/s2．求：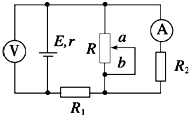
（2011?闵行区二模）电动势为E、内阻为r的电源与定值电阻R1、R2及滑动变阻器R连接成如图所示的电路，当滑动变阻器的触头由中点滑向b端时，下列说法正确的是（ ）