题目内容
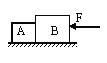
【题目】如图所示,质量为M=10㎏、长度为L=1m 、上表面光滑的长木板在水平恒定拉力F=50N的作用下,以速度v0= 5.5m/s沿水平地面向右做匀速直线运动。现有足够多的小铁块(可看作质点),它们的质量均为m=1kg,将第一个铁块无初速地放在木板的最右端,当第一个铁块离开木板的同时,又在木板最右端无初速放上第二个,只要前一个刚离开,就接着无初速放上另一个。
![]()
(1)板与地面间的动摩擦因数;
(2)最终第几个铁块能留在木板上,留在木板上的铁块离木板最右端多远?(g=10m/s2)
【答案】(1)0.5(2)第31个,0.25m
【解析】
(1)开始时刻,木板在拉力F作用下做匀速直线运动,由平衡条件即可求解动摩擦因数,(2)长木板做匀加速直线运动,小铁块保持静止,根据牛顿第二定律列式求解加速度,根据速度位移关系公式列式求解位移,然后结合几何关系列式求解即可.
(1)开始时刻,木板在拉力F作用下做匀速直线运动
由平衡条件得:![]()
解得:![]()
(2)当将小铁块放到木板上后,木板将做匀减速直线运动,设加速度为a
由牛顿第二定律得:![]()
解得:![]()
设板减速到零时位移为x,则![]()
代入数据解得:![]()
因每运动L=1m释放一个小铁块,共释放![]()
n取整数,故n=31,最终第31个铁块能留在木板上
此时留在木板上的铁块离木板右端距离为![]()

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目