题目内容
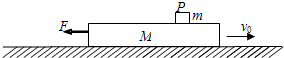 如图所示,长L=1.5m,质量M=10kg的长方体木箱,在水平面上向右做直线运动.当木箱的速度v0=3.6m/s时,对木箱施加一个方向水平向左的恒力F=50N,并同时将一个质量m=1kg的光滑小滑块轻放在距木箱右端1/3的P点(小滑块可视为质点,放在P点时相对于地面的速度为零),经过一段时间,小滑块脱离木箱落到地面.木箱与地面的动摩擦因数为μ=0.2,而小滑块与木箱之间的摩擦不计.取g=10m/s2,求:
如图所示,长L=1.5m,质量M=10kg的长方体木箱,在水平面上向右做直线运动.当木箱的速度v0=3.6m/s时,对木箱施加一个方向水平向左的恒力F=50N,并同时将一个质量m=1kg的光滑小滑块轻放在距木箱右端1/3的P点(小滑块可视为质点,放在P点时相对于地面的速度为零),经过一段时间,小滑块脱离木箱落到地面.木箱与地面的动摩擦因数为μ=0.2,而小滑块与木箱之间的摩擦不计.取g=10m/s2,求:(1)小滑块离开木箱时的小滑块的速度是多大;
(2)小滑块放上P点后,木箱向右运动的最大位移;
(3)小滑块离开木箱时的木箱的速度是多大.
分析:(1)木箱上表面的摩擦不计,因此小球在离开木箱前相对地面处于静止状态,离开木箱后将作自由落体运动,所以小滑块离开木箱时的速度是0;
(2)对木箱受力分析,求出加速度,可以根据速度-时间关系公式和位移-时间关系公式分别求出位移和时间;
(3)先对木箱受力分析,根据牛顿第二定律求得加速度,然后可以先根据位移-时间关系公式求得时间,再根据速度-时间公式求末速度,也可以直接根据速度位移关系公式求末速度.
(2)对木箱受力分析,求出加速度,可以根据速度-时间关系公式和位移-时间关系公式分别求出位移和时间;
(3)先对木箱受力分析,根据牛顿第二定律求得加速度,然后可以先根据位移-时间关系公式求得时间,再根据速度-时间公式求末速度,也可以直接根据速度位移关系公式求末速度.
解答:解:(1)木箱上表面的摩擦不计,因此小球在离开木箱前相对地面处于静止状态,离开木箱后将作自由落体运动.
所以小球离开木箱时速度为零
(2)小球放上木箱后相对地面静止,木箱的加速度
由F=μN=Ma1
N=(M+m)g
得:a1=
=
=7.2m/s2
木箱向右运动的最大位移
x1=
=
m=0.9m
小球放上P点后,木箱向右运动的最大位移为0.9m.
(3)由于x1小于1m,所以小球不会从木箱的左端掉下
木箱向左运动的加速度为
a2=
=
=2.8m/s2
设木箱向左运动x2时,小球从木箱的右端掉下
x2=x1+
=0.9+0.5=1.4m
设木箱向左运动所用的时间为t2,则
由x2=
a2t22
得:
t2=1s
所以,小球离开木箱的瞬间,木箱的速度方向向左,大小为:v2=a2t2=2.8×1=2.8m/s.
答:(1)小滑块离开木箱时的小滑块的速度是0;
(2)小滑块放上P点后,木箱向右运动的最大位移为0.9m;
(3)小滑块离开木箱时的木箱的速度是2.8m/s.
所以小球离开木箱时速度为零
(2)小球放上木箱后相对地面静止,木箱的加速度
由F=μN=Ma1
N=(M+m)g
得:a1=
| F+μ(M+m)g |
| M |
| 50+0.2×(10+1)×10 |
| 10 |
木箱向右运动的最大位移
x1=
| v02 |
| 2a1 |
| 3.62 |
| 2×7.2 |
小球放上P点后,木箱向右运动的最大位移为0.9m.
(3)由于x1小于1m,所以小球不会从木箱的左端掉下
木箱向左运动的加速度为
a2=
| F-μ(M+m)g |
| M |
| 50-0.2×(10+1)×10 |
| 10 |
设木箱向左运动x2时,小球从木箱的右端掉下
x2=x1+
| L |
| 3 |
设木箱向左运动所用的时间为t2,则
由x2=
| 1 |
| 2 |
得:
t2=1s
所以,小球离开木箱的瞬间,木箱的速度方向向左,大小为:v2=a2t2=2.8×1=2.8m/s.
答:(1)小滑块离开木箱时的小滑块的速度是0;
(2)小滑块放上P点后,木箱向右运动的最大位移为0.9m;
(3)小滑块离开木箱时的木箱的速度是2.8m/s.
点评:本题关键对分向右减速和向左加速两过程对木箱受力分析后求得加速度,然后根据运动学公式求解待求量.

练习册系列答案
相关题目
 如图所示,长L=1.6m,质量M=3kg的木板静放在光滑水平面上,质量m=1kg、带电量q=+2.5×10-4C的小滑块放在木板的右端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向竖直向下强度为E=4.0×104N/C的匀强电场,如图所示,现对木板施加一水平向右的拉力F.取g=10m/s2,求:
如图所示,长L=1.6m,质量M=3kg的木板静放在光滑水平面上,质量m=1kg、带电量q=+2.5×10-4C的小滑块放在木板的右端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向竖直向下强度为E=4.0×104N/C的匀强电场,如图所示,现对木板施加一水平向右的拉力F.取g=10m/s2,求: 如图所示,长L=1.2m、质量M=3kg的木板放在倾角为37°的光滑斜面上,质量m=1kg、带电荷量q=+2.5×10-4 C的物块放在木板的上端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向垂直斜面向下、场强E=4.0×104 N/C的匀强电场.现对木板施加一平行于斜面向上的拉力F=10.8N.取g=10m/s2,斜面足够长.设图示位置木板和物块的速度均为零.试求:
如图所示,长L=1.2m、质量M=3kg的木板放在倾角为37°的光滑斜面上,质量m=1kg、带电荷量q=+2.5×10-4 C的物块放在木板的上端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向垂直斜面向下、场强E=4.0×104 N/C的匀强电场.现对木板施加一平行于斜面向上的拉力F=10.8N.取g=10m/s2,斜面足够长.设图示位置木板和物块的速度均为零.试求: (2012?丰台区模拟)如图所示,长L=1.3m,质量M=5.0kg的平板小车A静止在光滑的水平面上,小车左端放有质量m=1.0kg的木块B(可以看作质点),木块B与小车A之间的动摩擦因数μ=0.20,现用水平恒力F拉动木块B在小车A上滑行.求:
(2012?丰台区模拟)如图所示,长L=1.3m,质量M=5.0kg的平板小车A静止在光滑的水平面上,小车左端放有质量m=1.0kg的木块B(可以看作质点),木块B与小车A之间的动摩擦因数μ=0.20,现用水平恒力F拉动木块B在小车A上滑行.求: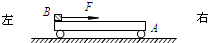 如图所示,长L=1.3m,质量M=5.0kg的平板小车A静止在光滑的水平面上,小车左端放有质量m=1.0kg的小木块B(可以看作质点),木块B与小车A之间的动摩擦因数μ=0.20,现用水平恒力F拉动木块B在小车A上滑行.求:
如图所示,长L=1.3m,质量M=5.0kg的平板小车A静止在光滑的水平面上,小车左端放有质量m=1.0kg的小木块B(可以看作质点),木块B与小车A之间的动摩擦因数μ=0.20,现用水平恒力F拉动木块B在小车A上滑行.求: 如图所示,长L=1.6m,质量M=3kg的木板静放在光滑水平面上,质量m=1kg的小物块放在木板的右端,木板和物块间的动摩擦因数μ=0.1.现对木板施加一水平向右的拉力F,取g=10m/s2,求:
如图所示,长L=1.6m,质量M=3kg的木板静放在光滑水平面上,质量m=1kg的小物块放在木板的右端,木板和物块间的动摩擦因数μ=0.1.现对木板施加一水平向右的拉力F,取g=10m/s2,求: