题目内容
 如图所示,传送带是绷紧的,原来传送带不动时,木块从顶端由静止开始自由下滑到底端所需时间为t1,若两轮顺时针转动,使传送带匀速运动,则木块从顶端由静止开始滑到底端所需时间为t2;若两轮逆时针转动,使传送带匀速运动,则木块从顶端由静止开始滑到底端所需时间为t3,木块与传送带间有摩擦,请比较t1、t2和t3的关系,则下列正确的是( )
如图所示,传送带是绷紧的,原来传送带不动时,木块从顶端由静止开始自由下滑到底端所需时间为t1,若两轮顺时针转动,使传送带匀速运动,则木块从顶端由静止开始滑到底端所需时间为t2;若两轮逆时针转动,使传送带匀速运动,则木块从顶端由静止开始滑到底端所需时间为t3,木块与传送带间有摩擦,请比较t1、t2和t3的关系,则下列正确的是( )分析:先分析传送带不动时物体的受力,根据牛顿第二定律和运动学公式得到,传送带的长度与时间、加速度的关系式;
再分析皮带向上或向下运动时物体的受力,由牛顿第二定律判断加速度的变化情况,由运动学公式判断时间关系.
再分析皮带向上或向下运动时物体的受力,由牛顿第二定律判断加速度的变化情况,由运动学公式判断时间关系.
解答:解:设传送带长度为L,倾角为α,物体与传送带间的动摩擦因数为μ.
传送带不动时物体受到重力、斜面的支持力和沿斜面向上的滑动摩擦力,根据牛顿第二定律得物体的加速度为:
a=
=g(sinα-μcosα)
且有L=
at12.
若两轮顺时针转动,物体所受的滑动摩擦力大小和方向没有改变,则加速度也不变,由L=
at22知,物块从顶端由静止开始滑到底端所需时间有关系:t2=t1.
若两轮逆时针转动,开始时受到重力、斜面的支持力和沿斜面向下的滑动摩擦力,根据牛顿第二定律得此时物体的加速度为:
a′=
=g(sinα+μcosα)
可见加速度增大,由公式L=
at32得知,t3一定小于t1.所以t2=t1>t3,故选B
故选:B.
传送带不动时物体受到重力、斜面的支持力和沿斜面向上的滑动摩擦力,根据牛顿第二定律得物体的加速度为:
a=
| mgsinα-μmgcosθ |
| m |
且有L=
| 1 |
| 2 |
若两轮顺时针转动,物体所受的滑动摩擦力大小和方向没有改变,则加速度也不变,由L=
| 1 |
| 2 |
若两轮逆时针转动,开始时受到重力、斜面的支持力和沿斜面向下的滑动摩擦力,根据牛顿第二定律得此时物体的加速度为:
a′=
| mgsinα+μmgcosθ |
| m |
可见加速度增大,由公式L=
| 1 |
| 2 |
故选:B.
点评:本题关键要正确分析物体所受的摩擦力,由牛顿第二定律研究加速度,根据运动学公式分析时间关系.

练习册系列答案
相关题目
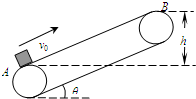 如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=2.5m/s的速率运行.将一质量m=1kg的工件(可看为质点)轻轻放在皮带的底端A点,工件能被传送到顶端B点,h=2.5m.已知工件与皮带间的动摩擦因数
如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=2.5m/s的速率运行.将一质量m=1kg的工件(可看为质点)轻轻放在皮带的底端A点,工件能被传送到顶端B点,h=2.5m.已知工件与皮带间的动摩擦因数 如图所示,绷紧的水平传送带始终以恒定速率v1运行.初速度大小为v2的小物块从与传送带等高的光滑水平地面上滑上传送带,以地面为参考系,v2>v1.从小物块滑上传送带开始计时,其v-t图象可能的是( )
如图所示,绷紧的水平传送带始终以恒定速率v1运行.初速度大小为v2的小物块从与传送带等高的光滑水平地面上滑上传送带,以地面为参考系,v2>v1.从小物块滑上传送带开始计时,其v-t图象可能的是( )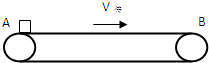 如图所示为车站使用的水平传送带装置模型,绷紧的传送带水平部分AB的长度L=5m,并以V传=2m/s的速度向右运动.现将一个可视为质点的旅行包轻轻地无初速地放在传送带的A端,已知旅行包与皮带之间的动摩擦因数μ=0.2.求:
如图所示为车站使用的水平传送带装置模型,绷紧的传送带水平部分AB的长度L=5m,并以V传=2m/s的速度向右运动.现将一个可视为质点的旅行包轻轻地无初速地放在传送带的A端,已知旅行包与皮带之间的动摩擦因数μ=0.2.求: