题目内容
 质量分别为M、m的物体用不计质量的细绳连接,放在水平面上.有一水平方向的力F作用在质量为m物体上,使两物体一起运动.求:
质量分别为M、m的物体用不计质量的细绳连接,放在水平面上.有一水平方向的力F作用在质量为m物体上,使两物体一起运动.求:(1)若水平面光滑,绳子的拉力;
(2)若两物体与水平面间的动摩擦因素皆为μ,求绳子的拉力.
分析:对两种情况分别研究:先利用整体法,可以根据牛顿第二定律求出整体运动的加速度的大小,再利用隔离法,对M研究可以求得细绳拉力的大小.
解答:解:(1)水平面光滑时,用水平恒力F拉A时,对于整体,由牛顿第二定律可得,F=(M+m)a,
对M受力分析可得,T=Ma=
(2)水平面粗糙时,对于整体:由牛顿第二定律可得,F-μ(M+m)g=(M+m)a′,
得a′=
-μg
对M:T′-μMg=Ma′
解得,T′=
答:
(1)若水平面光滑,绳子的拉力为
.
(2)若两物体与水平面间的动摩擦因素皆为μ,绳子的拉力为
.
对M受力分析可得,T=Ma=
| FM |
| M+m |
(2)水平面粗糙时,对于整体:由牛顿第二定律可得,F-μ(M+m)g=(M+m)a′,
得a′=
| F |
| M+m |
对M:T′-μMg=Ma′
解得,T′=
| FM |
| M+m |
答:
(1)若水平面光滑,绳子的拉力为
| FM |
| M+m |
(2)若两物体与水平面间的动摩擦因素皆为μ,绳子的拉力为
| FM |
| M+m |
点评:对于多个物体的受力分析通常采用的方法就是整体法和隔离法,通过整体法求得加速度,再利用隔离法求物体之间的内力的大小.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
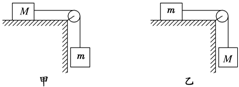 如图所示,质量分别为M和m的物块由相同的材料制成,且M>m,将它们用通过轻而光滑的定滑轮的细线连接.如果按图甲装置在水平桌面上,两物块刚好做匀速运动.如果互换两物块按图乙装置在同一水平桌面上,它们的共同加速度大小为( )
如图所示,质量分别为M和m的物块由相同的材料制成,且M>m,将它们用通过轻而光滑的定滑轮的细线连接.如果按图甲装置在水平桌面上,两物块刚好做匀速运动.如果互换两物块按图乙装置在同一水平桌面上,它们的共同加速度大小为( ) 如图所示,在粗糙的水平面上,质量分别为m和M的物块A、B用轻弹相连,两物块与水平面间的动摩擦因数均为?,当用水平力F作用于B上且两物块共同向右以加速度a1匀加速运动时,弹簧的伸长量为x1;当用同样大小的恒力F沿着倾角为θ的光滑斜面方向作用于B上且两物块共同以加速度a2匀加速沿斜面向上运动时,弹簧的伸长量为x2,则下列说法中正确的是( )
如图所示,在粗糙的水平面上,质量分别为m和M的物块A、B用轻弹相连,两物块与水平面间的动摩擦因数均为?,当用水平力F作用于B上且两物块共同向右以加速度a1匀加速运动时,弹簧的伸长量为x1;当用同样大小的恒力F沿着倾角为θ的光滑斜面方向作用于B上且两物块共同以加速度a2匀加速沿斜面向上运动时,弹簧的伸长量为x2,则下列说法中正确的是( ) 如图所示,用一根绕过定滑轮的细绳把质量分别为m和M的两个物块P和Q拴在一起,若将物块Q沿水平地面向右移动少许,仍能保持平衡,则关于力的变化的结论正确的是( )
如图所示,用一根绕过定滑轮的细绳把质量分别为m和M的两个物块P和Q拴在一起,若将物块Q沿水平地面向右移动少许,仍能保持平衡,则关于力的变化的结论正确的是( )