��Ŀ����
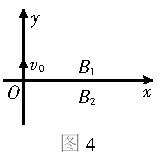
 ������Χ���ڴų�����̫�������Ĵ��������ڴ˴ų��е��˶���Ϊ��Ư�ƣ�������������һ�ּ���Ĵ�Ư���˶�����ij���������һ����������ӣ��������ƣ���x=0��y=0����y�������ٶ�v0�˶����ռ���ڴ�ֱֽ�����ǿ�ų�����y��0�������У��Ÿ�Ӧǿ��ΪB1����y��0�������У��Ÿ�Ӧǿ��ΪB2����B1 ��B2�ķ�����ͬ��B1��B2�������ڴų���������x��������Ư���˶�����ͼ��ʾ��
������Χ���ڴų�����̫�������Ĵ��������ڴ˴ų��е��˶���Ϊ��Ư�ƣ�������������һ�ּ���Ĵ�Ư���˶�����ij���������һ����������ӣ��������ƣ���x=0��y=0����y�������ٶ�v0�˶����ռ���ڴ�ֱֽ�����ǿ�ų�����y��0�������У��Ÿ�Ӧǿ��ΪB1����y��0�������У��Ÿ�Ӧǿ��ΪB2����B1 ��B2�ķ�����ͬ��B1��B2�������ڴų���������x��������Ư���˶�����ͼ��ʾ����1���ʣ��Ÿ�Ӧǿ��B1��B2�ķ�����Σ�
��2�������ӳ�����x=0����Ϊ��0��ͨ��x�ᣬ������2�ι�x��Ĺ����У���x�᷽���ƽ���ٶ�v��v0֮�ȣ�
��3���������ӳ�����x=0����Ϊ��0��ͨ��x�ᣬ������n�ι�x��Ĺ����У���x�᷽���ƽ���ٶ�v��v0֮�ȣ���nΪ������
��������������Ӵ�ֱ�ų��������Բ����ǿ�ų����������������ṩ������������켣�뾶r�����ڣ�����ƽ���ٶȵĶ����������2�ι�x��ʱ������x�᷽��Ư�Ƶ�ƽ���ٶȣ��Ӷ������x�᷽���ƽ���ٶ�v��v0֮�ȣ������Ƶķ����������n�ι�x��Ĺ����У���x�᷽���ƽ���ٶ�v��v0֮��
����⣺��1���������ֶ��������ܵ��������������ң����ԴŸ�Ӧǿ��B1��B2��ֱֽ�����⣮
��2����������ӵĵ����Ϊq������Ϊm����B1 ��B2���˶�����뾶�ֱ�Ϊr1��r2�����ڷֱ�ΪT1��T2����
qBv=m
��v=
��
r1=
��
r2=
��
T1=
��
T1=
��
���ӵ�2�ι�x�ᣬ��x���λ��x=2��r1-r2�� ��
�˶���ʱ��t=
(T1+T2) ��
ƽ���ٶ�v=
��
���ɢ٢ڢۢܢݢޢ�ʽ�ã�
=
��3�����ӵ�n�ι�x���λ��x=
?2r1-
?2r2 ��
������ʱ��t=
?
+
?
��
�����ߢ��ʽ��ã�
=
�𣺣�1���Ÿ�Ӧǿ��B1��B2�ķ���ֱֽ�����⣻
��2�������ӳ�����x=0����Ϊ��0��ͨ��x�ᣬ������2�ι�x��Ĺ����У���x�᷽���ƽ���ٶ�v��v0֮��Ϊ
��
��3���������ӳ�����x=0����Ϊ��0��ͨ��x�ᣬ������n�ι�x��Ĺ����У���x�᷽���ƽ���ٶ�v��v0֮��Ϊ
����n������
��2����������ӵĵ����Ϊq������Ϊm����B1 ��B2���˶�����뾶�ֱ�Ϊr1��r2�����ڷֱ�ΪT1��T2����
qBv=m
| v2 |
| r |
| 2��r |
| T |
r1=
| mv0 |
| qB1 |
r2=
| mv0 |
| qB2 |
T1=
| 2��m |
| qB1 |
T1=
| 2��m |
| qB2 |
���ӵ�2�ι�x�ᣬ��x���λ��x=2��r1-r2�� ��
�˶���ʱ��t=
| 1 |
| 2 |
ƽ���ٶ�v=
| x |
| t |
���ɢ٢ڢۢܢݢޢ�ʽ�ã�
| v |
| v0 |
| 2(B2-B1) |
| ��(B1+B2) |
��3�����ӵ�n�ι�x���λ��x=
| n+1 |
| 2 |
| n-1 |
| 2 |
������ʱ��t=
| n+1 |
| 2 |
| T1 |
| 2 |
| n-1 |
| 2 |
| T2 |
| 2 |
�����ߢ��ʽ��ã�
| v |
| v0 |
2[(n+1)
| ||
��[(n+1)
|
�𣺣�1���Ÿ�Ӧǿ��B1��B2�ķ���ֱֽ�����⣻
��2�������ӳ�����x=0����Ϊ��0��ͨ��x�ᣬ������2�ι�x��Ĺ����У���x�᷽���ƽ���ٶ�v��v0֮��Ϊ
| 2(B2-B1) |
| ��(B1+B2) |
��3���������ӳ�����x=0����Ϊ��0��ͨ��x�ᣬ������n�ι�x��Ĺ����У���x�᷽���ƽ���ٶ�v��v0֮��Ϊ
2[(n+1)
| ||
��[(n+1)
|
���������⿼����������ڴų��е��˶��İ뾶��ʽ�����ڹ�ʽ��Ӧ�ã��ӵ�0��ͨ��x�ᣬ����2�ι�x���˶���ʱ���������������ų����˶���ʱ��ͣ�

��ϰ��ϵ�д�
 ����������ϵ�д�
����������ϵ�д�
�����Ŀ