题目内容
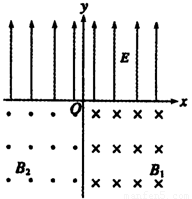
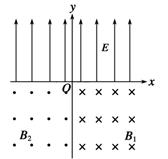
在xOy平面第Ⅰ、Ⅱ象限中，存在沿y轴正方向的匀强电场，场强为E＝
，在第Ⅲ、Ⅳ象限中，存在垂直于xOy平面方向的匀强磁场，如图11所示．磁感应强度B1＝B，B2＝2B.带电粒子a、b分别从第Ⅰ、Ⅱ象限的P、Q两点(图中没有标出)由静止释放，结果两粒子同时分别进入匀强磁场B1、B2中，再经过时间t第一次经过y轴时恰在点M(0，－
l)处发生正碰，碰撞前带电粒子b的速度方向与y轴正方向成60°角，不计粒子重力和两粒子间相互作用．求：
(1)两带电粒子的比荷及在磁场中运动的轨道半径；
(2)带电粒子释放的位置P、Q两点坐标及释放的时间差．
答案(1) 2l (2) 
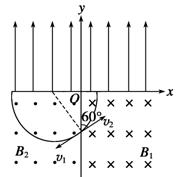
解析 (1)粒子运动轨迹如图．两粒子在磁场中运动时间相等且为t，即t1＝t2＝t
而t1＝
＝
，t2＝
＝
代入B2＝2B1＝2B得
＝
＝
由几何关系知R1＝R2＝
＝2l
(2)由qvB＝m
得v＝
所以v1＝
＝
得v2＝
＝
由Eqy＝
mv2得y＝
所以y1＝
＝2l, y2＝
＝8l
由几何关系知x1＝R－Rcos 60°＝l,
x2＝－(R＋Rcos 60°)＝－3l
所以P、Q的坐标分别为P(l,2l)、Q(－3l,8l).
粒子在电场中运动的时间为t＝
其中加速度a＝
＝
故两粒子由静止释放的时间差Δt＝
(v2－v1)＝
练习册系列答案
提分百分百检测卷系列答案
相关题目
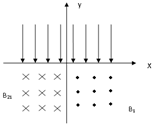在xoy 平面第Ⅰ、Ⅱ象限中，存在沿y轴负方向的匀强电场，场强为E=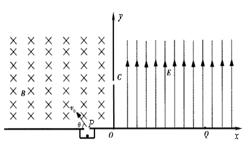
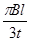，发生衰变生成新核
，放出一个质量为m，电荷量为－q的带电粒子。带电粒子从P孔以初速度v0沿垂直于磁场方向进入匀强磁场中，初速度方向与－x轴的夹角θ=60°，粒子恰好从C孔垂直于y轴射入匀强电场，最后打在Q点，已知OQ=2OC，不计粒子的重力，
，在第Ⅲ、Ⅳ象限中,存在垂直于xoy平面方向如图所示的匀强磁场，磁感应强度B2 =" 2" B1 =" 2" B ，带电粒子a、b先后从第Ⅰ、Ⅱ象限的P、Q两点（图中没有标出）由静止释放，结果两粒子同时进入匀强磁场B1、B2中，再经过时间t第一次经过y轴时恰在点M(0,-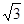
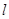)处发生正碰（即碰前两粒子速度方向相反），碰撞前带电粒子b的速度方向与y 轴正方向成60°角，不计粒子重力和两粒子间相互作用。求：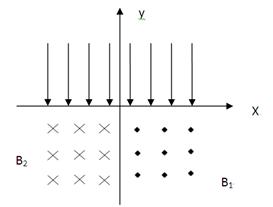
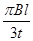，在第Ⅲ、Ⅳ象限中，存在垂直于xOy平面方向的匀强磁场,如图所示,磁感应强度B1＝B，B2＝2B．带电粒子a、b分别从第Ⅰ、Ⅱ象限的P、Q两点（图中没有标出）由静止释放，结果两粒子同时分别进入匀强磁场B1、B2中，再经过时间t第一次经过y轴时恰在点M（0，－
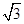l）处发生碰撞，碰撞时两粒子的速度在同一直线上，碰撞前带电粒子b的速度方向与y轴正方向成60°角，不计粒子重力和两粒子间相互作用．求：