题目内容
在倾角θ=30°的斜面上,固定一金属框,宽L=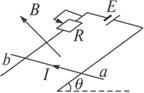
图
解析:设滑动变阻器阻值为R1时,金属棒刚好不下滑,金属棒平衡有:
F安+f=mgsinθ ①
N=mgcosθ ②
又F安=BIL ③
I=![]() ④
④
f=μN ⑤
②③④⑤代入①得:![]() +μmgcosθ=mgsinθ ⑥
+μmgcosθ=mgsinθ ⑥
代入数据,解得R1=4.8 Ω
设滑动变阻器阻值为R2时,金属棒也刚好不上滑,同理有:
F安=mgsinθ+f N=mgcosθ
F安=BIL I=![]() f=μN
f=μN
![]() =mgsinθ+μmgcosθ
=mgsinθ+μmgcosθ
代入数据,解得R2=1.6 Ω
所以当1.6 Ω≤R≤4.8 Ω时金属棒可静止在框架上.
答案:1.6 Ω≤R≤4.8 Ω

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2011?海淀区二模)如图所示,物体A、B的质量分别为mA、mB,且mA>mB.二者用细绳连接后跨过定滑轮,A静止在倾角θ=30°的斜面上,B悬挂着,且斜面上方的细绳与斜面平行.若将斜面倾角θ缓慢增大到45°,物体A仍保持静止.不计滑轮摩擦.则下列判断正确的是( )
(2011?海淀区二模)如图所示,物体A、B的质量分别为mA、mB,且mA>mB.二者用细绳连接后跨过定滑轮,A静止在倾角θ=30°的斜面上,B悬挂着,且斜面上方的细绳与斜面平行.若将斜面倾角θ缓慢增大到45°,物体A仍保持静止.不计滑轮摩擦.则下列判断正确的是( ) (2004?南通模拟)在倾角θ=30°的斜面上,固定一金属框,宽L=0.25m,接入电动势E=12V、内阻不计的电池.垂直框面放有一根质量m=0.2kg的金属棒ab,它与框架的动摩擦因数为
(2004?南通模拟)在倾角θ=30°的斜面上,固定一金属框,宽L=0.25m,接入电动势E=12V、内阻不计的电池.垂直框面放有一根质量m=0.2kg的金属棒ab,它与框架的动摩擦因数为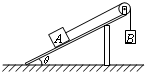 (2011?海淀区二模)如图所示,物体A、B的质量分别为mA、mB,且mB<mA<2mB.A和B用细绳连接后跨过光滑的定滑轮,A静止在倾角θ=30°的斜面上,且细绳平行于斜面.若将斜面倾角θ缓慢增大,在此过程中物体A先保持静止,到达一定角度后又沿斜面下滑,则下列判断正确的是( )
(2011?海淀区二模)如图所示,物体A、B的质量分别为mA、mB,且mB<mA<2mB.A和B用细绳连接后跨过光滑的定滑轮,A静止在倾角θ=30°的斜面上,且细绳平行于斜面.若将斜面倾角θ缓慢增大,在此过程中物体A先保持静止,到达一定角度后又沿斜面下滑,则下列判断正确的是( )