题目内容
在光滑的水平面上有三个完全相同的小球A、B、C用细绳连接起来，绳子OA=AB=BC，它们以O为圆心在水平面上以共同的角速度作匀速圆周运动，在运动中若绳子OA、AB、BC上的张力分别是T1、T2、T3那么T1：T2：T3是（ ）分析：三个小球均做匀速圆周运动具有相同的角速度，用隔离的方法单独研究每个小球，分别用牛顿第二定律解题．
解答：解：设OA长度为R，选C球为研究对象：水平方向仅受向左的绳子拉力T3，
由牛顿第二定律得：T3=mω23R
B物体水平方向受到向左的拉力T2，向右的拉力T3，
由牛顿第二定律得：T2-T3=mω22R
A物体水平方向受到向左的拉力T1，向右的拉力T2，
由牛顿定律得：T1-T2=mω2R
解得：T1：T2：T3=6：5：3
故选：D
由牛顿第二定律得：T3=mω23R
B物体水平方向受到向左的拉力T2，向右的拉力T3，
由牛顿第二定律得：T2-T3=mω22R
A物体水平方向受到向左的拉力T1，向右的拉力T2，
由牛顿定律得：T1-T2=mω2R
解得：T1：T2：T3=6：5：3
故选：D
点评：对与连接体问题应用整体法与隔离相结合的方法可以使题目变得易解，比如T1的解法选三小球为整体法更简单．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
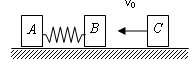
如图所示，在光滑的水平面上有三个小物块A、B、C，三者处于同一直线上，质量分别为mA=3m、mB=m、mC=m，初始A、B用轻弹簧栓连处于静止状态，C以初速度v0向左运动，B、C相碰后以相同速度向左运动但不粘连，求弹簧伸长量最大时储存的弹性势能EP．
v0
v0
v0
v0
v0
v0