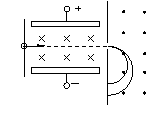题目内容
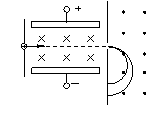
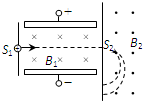 如图所示,一束具有各种速率的两种质量数不同的一价铜离子,水平地经过小孔S1射入垂直的匀强电场和匀强磁场区域,已知匀强电场的场强E=1×105V/m,匀强磁场的磁感应强度为B1=0.4T.求:
如图所示,一束具有各种速率的两种质量数不同的一价铜离子,水平地经过小孔S1射入垂直的匀强电场和匀强磁场区域,已知匀强电场的场强E=1×105V/m,匀强磁场的磁感应强度为B1=0.4T.求:(1)速度多大的一价铜离子,才能通过与S1小孔正对的S2小孔射入另一匀强磁场B2中?
(2)如果这些一价铜离子在匀强磁场B2中发生偏转后,打在过小孔S2且与两磁场分界面重合的照相底片上,已知分界面与小孔S1、S2连线垂直,若感光点到小孔S2的距离分别为d1=0.654m和d2=0.674m,那么对应的两种铜离子的质量数之比为多大?
分析:(1)根据电场力与洛伦兹力相平衡,可得速度大小;
(2)离子做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律,可得质量表达式,从而即可求解.
(2)离子做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律,可得质量表达式,从而即可求解.
解答:解:(1)从速度选择器中能通过小孔S2的离子,应满足qE=qvB1①
代入数据解得 v=2.5×105m/s ②
(2)设两种铜离子的质量数分别为M1和M2,质子的质量为mp,由题知质量为m的铜离子由S2进入偏转磁场后作匀速圆周运动,此时有qB2v=
=
③
则m=
④
所以质量数为 M=
=
⑤
故,对应的两种铜离子质量数之比为
=
=
⑥
代入数据解得
=
答:(1)速度为2.5×105m/s的一价铜离子,才能通过与S1小孔正对的S2小孔射入另一匀强磁场B2中;
(2)如果这些一价铜离子在匀强磁场B2中发生偏转后,打在过小孔S2且与两磁场分界面重合的照相底片上,已知分界面与小孔S1、S2连线垂直,若感光点到小孔S2的距离分别为d1=0.654m和d2=0.674m,那么对应的两种铜离子的质量数之比为
.
代入数据解得 v=2.5×105m/s ②
(2)设两种铜离子的质量数分别为M1和M2,质子的质量为mp,由题知质量为m的铜离子由S2进入偏转磁场后作匀速圆周运动,此时有qB2v=
| mv2 |
| R |
| mv2 |
| d/2 |
则m=
| dqB2 |
| 2v |
所以质量数为 M=
| m |
| mp |
| dqB2 |
| mp2v |
故,对应的两种铜离子质量数之比为
| M1 |
| M2 |
| (d1qB2)/(mp2v) |
| d2qB2/(mp2v) |
| d1 |
| d2 |
代入数据解得
| M1 |
| M2 |
| 654 |
| 674 |
答:(1)速度为2.5×105m/s的一价铜离子,才能通过与S1小孔正对的S2小孔射入另一匀强磁场B2中;
(2)如果这些一价铜离子在匀强磁场B2中发生偏转后,打在过小孔S2且与两磁场分界面重合的照相底片上,已知分界面与小孔S1、S2连线垂直,若感光点到小孔S2的距离分别为d1=0.654m和d2=0.674m,那么对应的两种铜离子的质量数之比为
| 654 |
| 674 |
点评:考查电场力与磁场力相平衡的匀速直线运动,也学会洛伦兹力使离子做匀速圆周运动,掌握平衡方程与牛顿第二定律方程,本题难度适中.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图所示,一束具有各种速率的两种质量数不同的一价铜离子,水平地经过小孔S1射入互相垂直的匀强电场(E=1.0×105V/m)和匀强磁场(B1=0.4T)区域,问:速度多大的一价铜离子,才能通过S1小孔正对的S2小孔射入另一匀强磁场(B2=0.5T)中,如果这些一价铜离子在匀强磁场B2中发生偏转后,打在小孔S2正下方的照相底片上,感光点到小孔S2的距离分别为0.654m和0.674m,那么对应的两种铜离子的质量数各为多少?假设一个质子的质量mp是1.66×10-27kg,不计重力.
如图所示,一束具有各种速率的两种质量数不同的一价铜离子,水平地经过小孔S1射入互相垂直的匀强电场(E=1.0×105V/m)和匀强磁场(B1=0.4T)区域,问:速度多大的一价铜离子,才能通过S1小孔正对的S2小孔射入另一匀强磁场(B2=0.5T)中,如果这些一价铜离子在匀强磁场B2中发生偏转后,打在小孔S2正下方的照相底片上,感光点到小孔S2的距离分别为0.654m和0.674m,那么对应的两种铜离子的质量数各为多少?假设一个质子的质量mp是1.66×10-27kg,不计重力.