题目内容
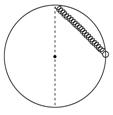
劲度系数为k的轻质弹簧，下端挂质量为m的小球，小球静止时离地面高为h，用力向下拉球使之与地面接触，而后从静止放开小球（弹簧未超过弹性限度）则（ ）
分析：A、球上升到最高点时，速度为零，根据对称性即可判断．
B、根据动能的变化判断系统势能的变化．
C、根据小球的受力判断小球的运动情况，找出何位置速度最大．
D、在最高点和最低点，小球所受的合力最大，加速度最大．
B、根据动能的变化判断系统势能的变化．
C、根据小球的受力判断小球的运动情况，找出何位置速度最大．
D、在最高点和最低点，小球所受的合力最大，加速度最大．
解答：解：A、球上升到最高点时，速度为零，根据对称性可知，弹簧的伸长量为h，所以距地面的最大高度为2h，故A正确．
B、在上升的过程中，先做加速度逐渐减小的加速运动，然后做加速度增大的减速运动，动能先增大后减小，所以系统势能先减小后增大．故B错误．
C、当加速度为零时，速度最大，该位置在平衡位置，距离地面的高度为h．故C正确．
D、在最低点，小球受重力和弹力，合力最大，F合=kh，根据牛顿第二定律，则最大加速度a=
．故D正确．
故选ACD
B、在上升的过程中，先做加速度逐渐减小的加速运动，然后做加速度增大的减速运动，动能先增大后减小，所以系统势能先减小后增大．故B错误．
C、当加速度为零时，速度最大，该位置在平衡位置，距离地面的高度为h．故C正确．
D、在最低点，小球受重力和弹力，合力最大，F合=kh，根据牛顿第二定律，则最大加速度a=
| kh |
| m |
故选ACD
点评：解决本题的关键知道在运动过程中，动能、重力势能、弹性势能相互转化，系统机械能守恒．在平衡位置速度最大，在最高点和最低点，加速度最大．
练习册系列答案
相关题目
和撞击速度v的关系．
时,装置可安全工作. 一质量为m 的小车若以速度v0 撞击弹簧,将导致轻杆向右移动
. 轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.
