题目内容
如图所示，在半径为R的圆形边界内存在竖直向上的匀强电场，电场强度E=1×106T。以圆心为坐标原点建立直角坐标系，在坐标原点分别以竖直向上、竖直向下，水平向左、水平向右同时抛出四个带正电的小球，小球的电荷量q=8×10-12C，质量m=1×10-6kg，它们的初速度大小均为v0=4m/s，忽略空气阻力，重力加速度g=10m/ s2。则：
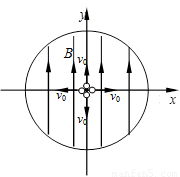
（1）当R=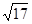
m时，水平向右抛出的小球经过多少时间到达圆形边界？
（2）试证明，在四个小球都未到达圆形边界前，能用一个圆将四个小球连起来。并写出圆心的坐标。
【答案】
（1）1s；（2）（0，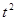
）
【解析】（16分）（1）小球所受电场力 
（1分）
合力 
（1分）
加速度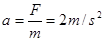 
，方向向下 （1分）
由水平向右的小球类平抛运动，可得：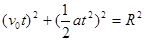
（2分）
得：
（1分）
（2）上抛小球位移的位移：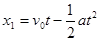
（1分）
下抛小球位移的位移：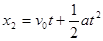
（1分）
两小球的竖直间距：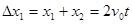
（1分）
水平抛出的小球，在竖直方向位移相同，水向方向的位移为
向左抛小球水平向左：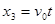
（1分）
向右抛小球水平向右：
（1分）
两小球的水平间距：
（1分）
由上述计算可知，两两小球的连线相互垂直，长度相等，且相互平分，如图所示，于是四个小球可用一个圆边接。 （2分）
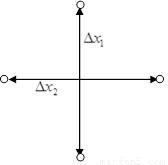
圆心坐标（0，）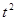
（2分）
（其它证明正确也对应给分）
练习册系列答案
相关题目
如图所示，在半径为R的圆形区域内，有匀强磁场，磁感应强度为B，方向垂直于圆平面（未画出）．一群比荷都为α的负离子体以相同速率v0（较大），由P点在纸平面内向不同方向射入磁场中发生偏转后，又飞出磁场，则下列说法正确的是（不计重力） （ ）
如图所示，在半径为R的圆内有一磁感应强度为B的向外的匀强磁场，一质量为m、电量为q的粒子（不计重力），从A点对着圆心方向垂直射入磁场，从C点飞出，则下列说法不正确的是（ ）
（2013?南宁三模）如图所示，在半径为R的圆形区域内有一匀强磁场，磁感应强度为B，方向垂直圆面向内．有一个质量为m，带电量为q的粒子，从A点沿半径方向垂直射人磁场内，又从C点射出，∠AOC=120°，下列说法正确的是（ ）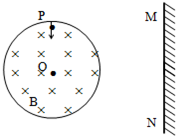
如图所示，在半径为R=
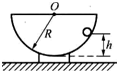如图所示，在半径为R的半圆形碗的光滑表面上，一质量为m的小球以角速度ω在水平面内作匀速圆周运动，此时球对碗的压力FN=