题目内容
如图所示,光滑水平面AB与竖直面的半圆形导轨在B点相连接,导轨半径为R,一个质量为m的静止的木块在A处压缩弹簧,释放后,木块获得向右的初速度,当它经过B点进入半圆形导轨瞬间对导轨的压力是其重力的7倍,之后向上运动恰能通过轨道最高点C,试求:
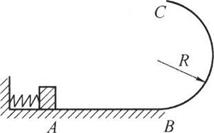
(1)木块到达B处时的速度大小;
(2)木块释放前,弹簧所具有的弹性势能;
(3)木块从B到C过程中克服摩擦力所做的功。

(1)木块到达B处时的速度大小;
(2)木块释放前,弹簧所具有的弹性势能;
(3)木块从B到C过程中克服摩擦力所做的功。
(1)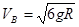 (2)
(2)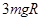 (3)
(3)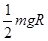
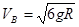 (2)
(2)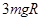 (3)
(3)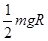
试题分析:(1)根据牛顿第二定律可得:
 解得
解得 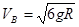 (3分)
(3分)(2)弹簧的弹性势能全部转化为物体的动能,故有:
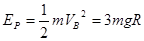 (3分)
(3分)(3)在C点:
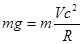
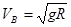 (3分)
(3分)B→C过程中:
 (3分)
(3分)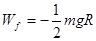 克服阻力做功
克服阻力做功 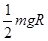 (2分)
(2分) 点评:对于圆周运动的受力问题,我们要找出向心力的来源.动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.

练习册系列答案
相关题目
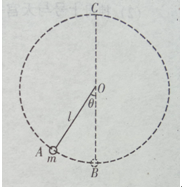
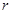 的半球形金属球壳滑到最低点时的速度大小为
的半球形金属球壳滑到最低点时的速度大小为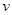 ,如图所示,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )
,如图所示,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )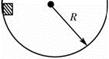
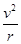
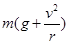
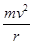
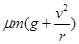
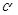 次方成正比
次方成正比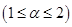 。假设一个大雨滴和一个小雨滴从同一云层同时下落,最终它们都 (填“加速”、“减速”或“匀速”)下落。 (填“大”或“小”)雨滴先落到地面;接近地面时, (填“大”或“小”)雨滴的速度较小。
。假设一个大雨滴和一个小雨滴从同一云层同时下落,最终它们都 (填“加速”、“减速”或“匀速”)下落。 (填“大”或“小”)雨滴先落到地面;接近地面时, (填“大”或“小”)雨滴的速度较小。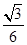 ,槽内靠近右侧壁处有一小物块A(可视为质点),它到凹槽左侧壁的距离
,槽内靠近右侧壁处有一小物块A(可视为质点),它到凹槽左侧壁的距离
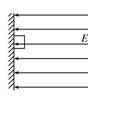
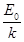 ,物体在竖直墙壁上的位移达最大值
,物体在竖直墙壁上的位移达最大值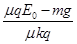 ,物体运动速度达最大值
,物体运动速度达最大值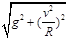 B.m
B.m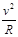 C.m
C.m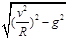 D.mg
D.mg