Question

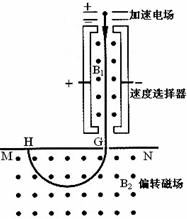
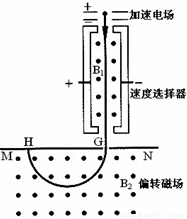
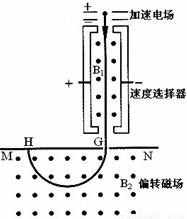
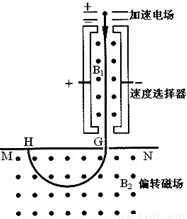
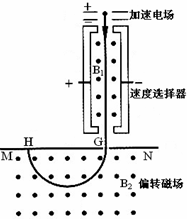如图为质谱仪的原理图．电荷量为q、质量为m的带正电粒子从静止开始经过电压为U的加速电场加速后，进入粒子速度选择器，选择器中存在相互垂直的匀强电场和匀强磁场，匀强电场的场强为E，方向水平向右．已知带电粒子能够沿直线穿过速度选择器，从G点垂直于MN进入偏转磁场．该偏转磁场是一个以直线MN为上边界、方向垂直于纸面向外的匀强磁场．带电粒子经偏转磁场后，最终到达照相底片上的H点．测得G、H间的距离为L，粒子的重力可忽略不计．求：
（1）粒子从加速电场射出时速度v的大小；
（2）速度选择器中匀强磁场的磁感应强度B₁的大小；
（3）偏转磁场的磁感应强度B₂的大小．

Answer 1

分析：（1）粒子在电场中运动只有电场力做功，根据动能定理可以求得粒子从加速电场射出时速度v的大小；
（2）带电的粒子在速度选择器中做匀速直线运动，说明粒子受力平衡，根据粒子的受力状态可以求得速度选择器中匀强磁场的磁感应强度B₁的大小；
（3）粒子在磁场中做匀速圆周运动，根据粒子在磁场中运动的半径公式可以求得偏转磁场的磁感应强度B₂的大小．

解答：解：（1）粒子在电场中运动只有电场力做功，
根据动能定理可得，
qU=

1

2

mv²
可以求得粒子从加速电场射出时速度v的大小v为，
v=

2qU m

；
（2）粒子在速度选择器中受力平衡，
所以qE=qvB₁，
所以磁感应强度B₁的大小为
B₁=

E

v

=E

m 2qU

，
（3）粒子垂直进入磁场，做圆周运动，半径的大小为

1

2

L，
所以qvB₂=m

v2

r

即

1

2

L=

mv

qB2

，
所以B2=

2

l

2mU q

．

点评：粒子在速度选择器中的运动可以分为匀加速直线运动、匀速运动和匀速圆周运动，根据不同阶段的运动的特点来分类解决．