题目内容
一辆正沿平直路面行驶的车厢内,一个面向车前进方向站立的人对车厢壁施加水平推力F,在车前进s的过程中,下列说法正确的是: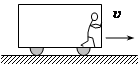
| A.当车匀速前进时,人对车做的总功为正功 |
| B.当车加速前进时,人对车做的总功为负功 |
| C.当车减速前进时,人对车做的总功为负功 |
| D.不管车如何运动,人对车做的总功都为零 |
B
解析试题分析:人对车施加了三个力,分别是推力F、静摩擦力f、压力,其中推力F和静摩擦力f分别发生了相同的位移,做了正功和负功。当车匀速时,先对人分析,人匀速,两反作用力 和
和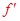 相等,
相等,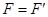 ,
,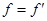 ,则人对车做的总功为零,选项A错误。人加速时,
,则人对车做的总功为零,选项A错误。人加速时,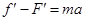 ,有
,有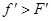 ,静摩擦力做功大些,故人对车做的总功为负功,选项B正确。人减速时,
,静摩擦力做功大些,故人对车做的总功为负功,选项B正确。人减速时,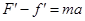 ,
, ,推力做正功更多,人对车做的总功为正功,选项C错误。人对车做的总功与人的运动状态(即车的运动)有关,选项D错误。
,推力做正功更多,人对车做的总功为正功,选项C错误。人对车做的总功与人的运动状态(即车的运动)有关,选项D错误。
考点:本题考查了功的定义、牛顿第二定律、牛顿第三定律。

如图,质量为m的小球与轻质弹簧Ⅰ和水平轻绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q,当剪断Ⅱ的瞬间,小球的加速度a应是
| A.大小a=g |
B.大小a="g" tan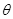 |
| C.方向水平向左 |
| D.方向竖直向下 |
如图所示,甲、乙两车均在光滑的水平面上,质量都是 ,人的质量都是
,人的质量都是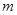 ,甲车上人用力
,甲车上人用力 推车,乙车上的人用等大的力
推车,乙车上的人用等大的力 拉绳子(绳与轮的质量和摩擦均不计);人与车始终保持相对静止.下列说法正确的是
拉绳子(绳与轮的质量和摩擦均不计);人与车始终保持相对静止.下列说法正确的是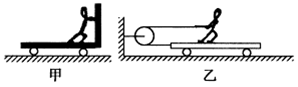
A.甲车的加速度大小为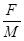 |
| B.甲车的加速度大小为0 |
C.乙车的加速度大小为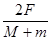 |
| D.乙车的加速度大小为0 |
如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,由此可以确定
| A.滑块下滑和上滑过程加速度的大小a1、a2 |
| B.滑块最终所处的位置 |
| C.滑块与杆之间动摩擦因数μ |
| D.滑块第k次与挡板碰撞后速度vk |
将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动。用频闪照相机拍到如图所示的单摆运动过程的频闪照片,以下说法正确的是
| A.摆线碰到障碍物前后的周期之比为3:2. |
| B.摆线碰到障碍物前后的摆长之比为3:2 |
| C.摆球经过最低点时,线速度变小,半径减小,摆线张力变大 |
| D.摆球经过最低点时,角速度变大,半径减小,摆线张力不变 |
如图所示,三个质量相同,形状相同的斜面,放在地面上。另有三个质量相同的小物体分别从斜面顶端沿斜面滑下。由于小物体跟斜面间的摩擦不同,第一个小物体匀加速下滑;第二个小物体匀速下滑;第三个小物体以初速v0匀减速下滑。三个斜面都不动。则下滑过程中斜面对地面的压力大小顺序是( )
| A.N1 = N2 = N3 | B.N1 < N2 < N3 | C.N1 > N2 > N3 | D.N1 < N2 = N3 |
 表示物块的加速度大小,F表示水平拉力的大小。能正确描述F与
表示物块的加速度大小,F表示水平拉力的大小。能正确描述F与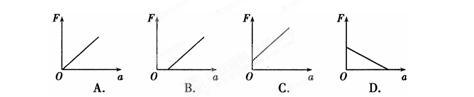


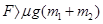 B.
B.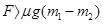
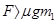 D.
D.