题目内容
如图所示为水平面内的两条相互平行的光滑金属导轨,电阻可以忽略不计,轨道间距为l。导轨所处水平面内存在着竖直方向的匀强磁场,磁感应强度为B。两导体杆a和b垂直于导轨放置,它们的质量分别为m和2m,电阻分别为r和2r。现给导体杆a一沿导轨方向的初速度v0,若两杆始终都只能沿导轨方向运动,且除匀强磁场外其他磁场不计,试求:当杆a的速度减为v0/2时
(1)两导体杆的加速度分别为多大?
(2)两杆上分别产生了多少焦耳热?
(3)已经有多少电量流过了杆a?两导体杆间距相比最初增加了多少?

(1)根据楞次定律,a杆受向左的安培力向右作减速运动,b杆受向右的安培力向右作加速运动,两杆受力等大反向,因此两杆系统动量守恒。当a杆的速度为v1=v0/2时,b杆的速度设为v2,有
mv1+2mv2=mv0 (2 分)
可得v2= v0/4
根据感应电动势规律可得此时两杆电动势
E1=Blv1= Blv0
Blv0
E2=Blv2= Blv0
Blv0
根据闭合回路欧姆定律,回路电路为

I=
根据安培力性质,两杆所受安培力大小为
F=BIl= (2分)
(2分)
根据牛顿第二定律,两杆加速度大小分别为
a1= =
= ,a2=
,a2= =
= (2分)
(2分)
(2)由于两杆的动能通过电磁感应转化为电能且由焦耳热方式放出,根据能量守恒,电路放出内能
Q= =
= (2分)
(2分)
因为两杆电流在任意时刻都相等,所以两杆发热量与电阻成正比,两杆分别产生热量
Q1= =
=
Q2= =
= (1分)
(1分)
(3)由安培力性质,杆受到的安培力
F=BIl
在一段很短的时间Δt内,由于电流可看做稳定,安培力产生冲量
Δτ=FΔt=BlΔq (2分)
其中Δq为时间Δt内通过电路的电量,因为B、l都不变,所以即使在较长时间内此式结果仍成立。
又根据动量定理,a杆受到的安培力冲量大小为
τ=mv0-mv1=
所以通过a杆的总电量
q= =
= (1分)
(1分)
由法拉第电磁感应定律,电路中的总电动势
E=
其中ΔS为电路面积的变化量,Δt为一段很短的时间
由闭合回路欧姆定律,电路中电流
I=
由电流与电量关系
Δq=IΔt
根据以上三式可得
Δq= (2分)
(2分)
因为B、r都不变,所以此式在一段较长时间内仍成立,因此电路面积增加量为
S=
两杆间距增加
x= (1分)
(1分)
【解析】略

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案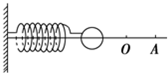 如图所示为水平面内振动的弹簧振子,O是平衡位置,A是最大位移处,不计小球与轴的摩擦,则下列说法正确的是( )
如图所示为水平面内振动的弹簧振子,O是平衡位置,A是最大位移处,不计小球与轴的摩擦,则下列说法正确的是( )| A、每次经过O点时的动能相同 | B、从A到O的过程中加速度不断增加 | C、从A到O的过程中速度不断增加 | D、从O到A的过程中速度与位移的方向相反 |

