题目内容
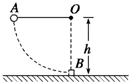 如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.物块B质量是小球的4倍,置于粗糙的水平面上且位于O点的正下方,物块与水平面间的动摩擦因数为μ.现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短),反弹后上升至最高点时到水平面的距离为h.小球与物块均视为质点,不计空气阻力,重力加速度为g,求:
如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.物块B质量是小球的4倍,置于粗糙的水平面上且位于O点的正下方,物块与水平面间的动摩擦因数为μ.现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短),反弹后上升至最高点时到水平面的距离为h.小球与物块均视为质点,不计空气阻力,重力加速度为g,求:①物块在水平面上滑行的时间t.
②通过计算判断A、B间碰撞为弹性碰撞还是非弹性碰撞.
分析:研究小球从水平位置运动到最低点,根据机械能守恒求出与物块碰撞前的速度大小.
碰撞后小球反弹,根据机械能守恒求出与物块碰撞后的速度大小.
碰撞过程,根据动量守恒求出碰撞后物块的速度大小,运用牛顿第二定律和运动学公式结合解决问.
求出碰撞前系统的总动能和碰撞后系统的总动能,进行比较判断A、B间碰撞为弹性碰撞还是非弹性碰撞.
碰撞后小球反弹,根据机械能守恒求出与物块碰撞后的速度大小.
碰撞过程,根据动量守恒求出碰撞后物块的速度大小,运用牛顿第二定律和运动学公式结合解决问.
求出碰撞前系统的总动能和碰撞后系统的总动能,进行比较判断A、B间碰撞为弹性碰撞还是非弹性碰撞.
解答:解:①.设小球的质量为m,运动到最低点与物块碰撞前的速度大小为v1,取小球运动到最低点重力势能为零,
根据机械能守恒定律,有mgh=
mv12①
得v1=
设碰撞后小球反弹的速度大小为v1',同理有mg
=
mv1′2②
得 v1′=
设碰撞后物块的速度大小为v2,取水平向右为正方向,根据动量守恒定律,有mv1=-mv1'+4mv2③
得v2=
④
物块在水平面上滑行所受摩擦力的大小:F=4μmg
根据牛顿第二定律,有:F=4ma⑤
设物块在水平面上滑行的时间为t,根据运动学公式,有t=
⑥
联立,解得:t=
⑦
②.碰撞前系统的总动能:Ek=
m
=mgh
碰撞后系统的总动能:
=
m
+
4m
=
mgh
由于Ek>Ek′,故此次碰撞为非弹性碰撞.
答:①物块在水平面上滑行的时间是
.
②此次碰撞为非弹性碰撞.
根据机械能守恒定律,有mgh=
| 1 |
| 2 |
得v1=
| 2gh |
设碰撞后小球反弹的速度大小为v1',同理有mg
| h |
| 9 |
| 1 |
| 2 |
得 v1′=
| ||
| 3 |
设碰撞后物块的速度大小为v2,取水平向右为正方向,根据动量守恒定律,有mv1=-mv1'+4mv2③
得v2=
| ||
| 3 |
物块在水平面上滑行所受摩擦力的大小:F=4μmg
根据牛顿第二定律,有:F=4ma⑤
设物块在水平面上滑行的时间为t,根据运动学公式,有t=
| v2 |
| a |
联立,解得:t=
| ||
| 3μg |
②.碰撞前系统的总动能:Ek=
| 1 |
| 2 |
| v | 2 1 |
碰撞后系统的总动能:
| E | ′ k |
| 1 |
| 2 |
| v′ | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 5 |
| 9 |
由于Ek>Ek′,故此次碰撞为非弹性碰撞.
答:①物块在水平面上滑行的时间是
| ||
| 3μg |
②此次碰撞为非弹性碰撞.
点评:本题关键是碰撞前A球机械能守恒,碰撞后A球机械能守恒,
撞过程两球系统动量也守恒,求出碰撞后物块的速度大小.
解决问题首先要清楚研究对象的运动过程.
撞过程两球系统动量也守恒,求出碰撞后物块的速度大小.
解决问题首先要清楚研究对象的运动过程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2010?天津)如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.物块B质量是小球的5倍,至于粗糙的水平面上且位于O点正下方,物块与水平面间的动摩擦因数为μ.现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短),反弹后上升至最高点时到水平面的距离为
(2010?天津)如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.物块B质量是小球的5倍,至于粗糙的水平面上且位于O点正下方,物块与水平面间的动摩擦因数为μ.现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短),反弹后上升至最高点时到水平面的距离为 。小球与物块均视为质点,不计空气阻力,重力加速度为g,求物块在水平面上滑行的时间t。
。小球与物块均视为质点,不计空气阻力,重力加速度为g,求物块在水平面上滑行的时间t。
 如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h。物块B质量是小球的5倍,至于粗糙的水平面上且位于O点正下方,物块与水平面间的动摩擦因数为μ。现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短),反弹后上升至最高点时到水平面的距离为
如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h。物块B质量是小球的5倍,至于粗糙的水平面上且位于O点正下方,物块与水平面间的动摩擦因数为μ。现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短),反弹后上升至最高点时到水平面的距离为 。小球与物块均视为质点,不计空气阻力,重力加速度为g,求物块在水平面上滑行的时间t。
。小球与物块均视为质点,不计空气阻力,重力加速度为g,求物块在水平面上滑行的时间t。