题目内容
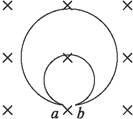
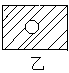
 如图12-1所示,有两块大小不同的圆形薄板(厚度不计),质量
如图12-1所示,有两块大小不同的圆形薄板(厚度不计),质量
分别为M和m,半径分别为R和r,两板之间用一根长为0.4m的轻
绳相连结。开始时,两板水平放置并叠合在一起,静止于高度为
0.2m处。然后自由下落到一固定支架C上,支架上有一半径为
R‘(r<R’<R)的圆孔,圆孔与两薄板中心均在圆板中心轴线上,木
板与支架发生没有机械能损失的碰撞。碰撞后,两板即分离,直到
轻绳绷紧。在轻绳绷紧的瞬间,两物体具有共同速度V,如图12-2所示。
求:(1)若M=m,则V值为多大 (2)若M/m=K,试讨论 V的方向与K值间的关系。
(1)V=![]()
(2)①K<3时,V>0,两板速度方向向下。
②K>3时,V<0,两板速度方向向上。
③K=3时,V=0,两板瞬时速度为零,接着再自由下落。
解析:
开始 M与m自由下落,机械能守恒。M与支架C碰撞后,M以原速率返回,向上做匀减速运动。m向下做匀加速运动。在绳绷紧瞬间,内力(绳拉力)很大,可忽略重力,认为在竖直方向上M与m系统动量守恒。(1)据机械能守恒:(M+m)gh=![]() (M+m)V02 所以,V0=
(M+m)V02 所以,V0=![]() =2m/s
=2m/s
M碰撞支架后以Vo返回作竖直上抛运动,m自由下落做匀加速运动。在绳绷紧瞬间,M速度为V1,上升高度为h1,m的速度为V2,下落高度为h2。则:
h1+h2=0.4m,h1=V0t-![]() gt2,h2=V0t+
gt2,h2=V0t+![]() gt2,而h1+h2=2V0t,
gt2,而h1+h2=2V0t,
故:![]()
所以:V1=V0-gt=2-10×0.1=1m/s V2=V0+gt=2+10×0.1=3m/s
根据动量守恒,取向下为正方向,mV2-MV1=(M+m)V,所以![]()
那么当m=M时,V=1m/s;当M/m=K时,V=![]() 。
。
讨论:①K<3时,V>0,两板速度方向向下。
②K>3时,V<0,两板速度方向向上。
③K=3时,V=0,两板瞬时速度为零,接着再自由下落。

 巧学巧练系列答案
巧学巧练系列答案